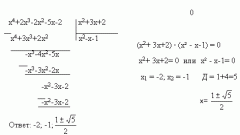Инструкция
1
Общий вид линейного дифференциального уравнения первого порядка таков:

y′ + p(x)*y = f(x),

где y — неизвестная функция, а p(x) и f(x) — некоторые заданные функции. Они считаются непрерывными в той области, в которой требуется проинтегрировать уравнение. В частности, они могут быть и константами.
2
Если f(x) ≡ 0, то уравнение называют однородным; если нет — то, соответственно, неоднородным.
3
Линейное однородное уравнение может быть решено методом разделения переменных. Его общий вид: y′ + p(x)*y = 0, следовательно:

dy/dx = -p(x)*y, откуда следует, что dy/y = -p(x)dx.
4
Интегрируя обе части получившегося равенства, получаем:

∫(dy/y) = - ∫p(x)dx, то есть ln(y) = - ∫p(x)dx + ln(C) или y = C*e^(- ∫p(x)dx)).
5
Решение неоднородного линейного уравнения можно вывести из решения соответствующего однородного, то есть того же самого уравнения с отброшенной правой частью f(x). Для этого нужно заменить константу C в решении однородного уравнения неизвестной функцией φ(x). Тогда решение неоднородного уравнения будет представлено в виде:

y = φ(x)*e^(-∫p(x)dx)).
6
Дифференцируя это выражение, получим, что производная от y равна:

y′ = φ′(x)*e^(- ∫p(x)dx) - φ(x)*p(x)* e^(- ∫p(x)dx).

Подставив найденные выражения для y и y′ в исходное уравнение и упростив полученное, легко прийти к результату:

dφ/dx = f(x)*e^( ∫p(x)dx).
7
После интегрирования обеих частей равенства оно получает вид:

φ(x) = ∫(f(x)*e^(∫p(x)dx))dx + C1.

Таким образом, искомая функция y выразится в виде:

y = e^(- ∫p(x)dx)*(C + ∫f(x)*e^(∫p(x)dx))dx).
8
Если приравнять постоянную C нулю, то из выражения для y можно получить частное решение заданного уравнения:

y1 = (e^(- ∫p(x)dx))*(∫f(x)*e^(∫p(x)dx))dx).

Тогда полное решение можно будет выразить в виде:

y = y1 + C*e^(- ∫p(x)dx)).
9
Иными словами, полное решение линейного неоднородного дифференциального уравнения первого порядка равно сумме его частного решения и общего решения соответствующего однородного линейного уравнения первого порядка.