Инструкция
1
Чтобы вычислить диагонали ромба, достаточно воспользоваться общеизвестной формулой, справедливой для любого четырехугольника. Она состоит в том, что сумма квадратов длин диагоналей равна квадрату стороны, умноженному на четыре:d1² + d2² = 4•a².
2
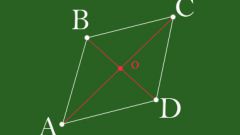
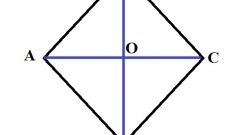
Облегчить решение геометрических задач с этой фигурой поможет знание некоторых свойств, присущих ромбу и связанных с длинами его диагоналей:• Ромб является частным случаем параллелограмма, следовательно, противолежащие стороны у него также попарно параллельны и равны;• Диагонали точкой пересечения делятся пополам, а угол между ними – прямой;• Каждая диагональ делит пополам углы, вершины которых соединяет, являясь их биссектрисами и одновременно медианами треугольников, образованных двумя смежными сторонами ромба и другой диагональю.
3
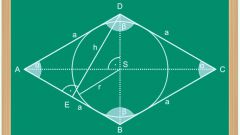
Формула для диагоналей является прямым следствием из теоремы Пифагора. Рассмотрите один из треугольников, получившихся в результате деления ромба диагоналями на четыре части. Он – прямоугольный, это вытекает из свойств диагоналей ромба, кроме того, длины катетов равны половинам диагоналей, а гипотенуза – это сторона ромба. Значит, согласно теореме:d1²/4 + d2²/4 = a² → d1² + d2² = 4•a².
4
В зависимости от начальных данных задачи, могут быть произведены дополнительные промежуточные действия, чтобы определить неизвестную величину. Например, найдите диагонали ромба, если известно, что одна из них превышает длину стороны на 3 см, а другая в полтора раза больше.
5
Решение.Выразите длины диагоналей через сторону, которая в данном случае неизвестна. Обозначьте ее за x, тогда: d1=x+3; d2=1,5•x.
6
Запишите формулу для диагоналей ромба:d1² + d2² = 4•a²
7
Подставьте полученные выражения и составьте уравнение с одной переменной:(x + 3)² + 9/4•x² = 4•x²
8
Приведите его к квадратному и решите:x² – 8•x – 12 = 0D = 64 + 48 = 110x1 = (8+√110)/2 ≈ 9,2; x2 ромба равна 9,2 см. Тогда d1 = 11,2 см; d2 = 13,8 см.