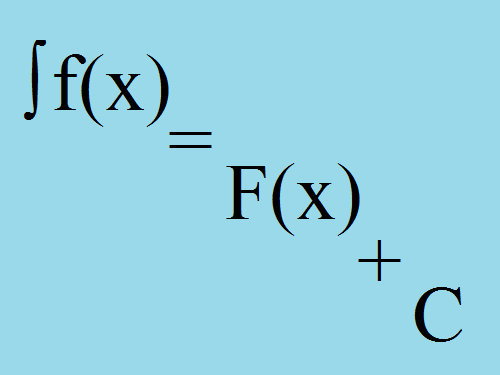Инструкция
1
Интеграл относится к понятиям математического анализа и графически представляет собой площадь криволинейной трапеции, ограниченной на оси абсцисс предельными точками интегрирования. Находить интеграл функции значительно сложнее, чем искать ее производную.
2
Существует несколько методов вычисления неопределенного интеграла: непосредственное интегрирование, введение под знак дифференциала, метод подстановки, интегрирование по частям, подстановка Вейерштрасса, теорема Ньютона-Лейбница и др.
3
Непосредственное интегрирование предполагает приведение с помощью простых преобразований исходного интеграла к табличному значению. Например:∫dy/(sin²y·cos²y) = ∫(cos²y + sin²y)/(sin²y·cos²y)dy = ∫dy/sin²y + ∫dy/cos²y = -ctgy + tgy + C.
4
Метод введения под знак дифференциала или замена переменной представляет собой постановку новой переменной. При этом исходный интеграл сводится к новому интегралу, который можно преобразовать к табличному виду методом непосредственного интегрирования:Пусть есть интеграл ∫f(y)dy = F(y) + C и некоторая переменная v = g(y), тогда:∫f(y)dy -> ∫f(v)dv = F(v) + C.
5
Следует запомнить некоторые простейшие подстановки для облегчения работы с этим методом:dy = d(y + b);ydy = 1/2·d(y² + b);sinydy = - d(cosy);cosydy = d(siny).
6
Пример:∫dy/(1 + 4·y²) = ∫dy/(1 + (2·y) ²) = [dy -> d(2·y)] = 1/2·∫d(2·y)/(1 + (2·y) ²) = 1/2·arctg2·y + C.
7
Интегрирование по частям производится по следующей формуле:∫udv = u·v - ∫vdu.Пример:∫y·sinydy = [u = y; v = siny] = y·(-cosy) – ∫(-cosy)dy = -y·cosy + siny + C.
8
Определенный интеграл в большинстве случаев находится по теореме Ньютона-Лейбница:∫f(y)dy на интервале [a; b] равен F(b) – F(a).Пример: Найдите ∫y·sinydy на интервале [0; 2π]:∫y·sinydy = [u = y; v = siny] = y·(-cosy) – ∫(-cosy)dy = (-2π·cos2π + sin2π) – (-0·cos0 + sin0) = -2π.
Видео по теме