Инструкция
1
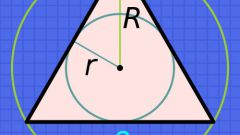
Посчитайте значение сторон треугольника. Достаточно часто в задачах можно встретить правильный треугольник, к примеру, со стороной a. Так как данный многоугольник является правильным (по условиям задачи), то все его стороны будут между собой равны. Следовательно, вы можете рассчитать все его стороны, зная величину медианы и высоту треугольника. Для этого используйте метод нахождения сторон при помощи косинуса: a=x:cosα, где а - стороны треугольника; x - это высота, биссектриса или медиана.
2
Определите аналогичным образом все неизвестные стороны (всего их три) в равнобедренном треугольнике, при заданной высоте. В свою очередь, она должна быть спроецирована на основании треугольника. Зная значение высоты основания x, вы сможете найти сторону равнобедренного треугольника: a=x/cosα. Потому как a=b, согласно условиям равнобедренного треугольника, вы можете определить его стороны по следующей формуле: a=b=x:cosα.
3
Найдите длину основания треугольника. Для этих целей можете использовать теорему Пифагора, это поможет вам определить половину необходимого значения основания:c:2=√(x:cosα)^2-(x^2)=√x^2 (1-cos^2α)/ cos^2α=xtgα.Далее определите длину основания: c=2xtgα.
4
Посчитайте стороны квадрата. В свою очередь, квадрат подразумевает под собой правильный четырехугольник, у которого можно вычислить стороны с помощью нескольких способов. Первый из которых предлагает нахождение сторон через диагональ квадрата. Потому как, все углы квадрата являются прямыми, данная диагональ разделяет их пополам и образует два одинаковых прямоугольных треугольника. Эти треугольники обладают углами, равными 45 градусам при основании. Таким образом, из всего вышесказанного ясно, что сторона квадрата будет равна: a=b=c=f=d*cosα=d√2/2, где d - значение диагонали квадрата.
5
В том случае, если квадрат расположен в окружности, то зная радиус данной окружности, вы можете найти его сторону. Для этого используйте следующую формулу: a4=R√2, где R является радиусом окружности.