Инструкция
1
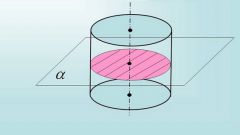
Круглый конус – тело, полученное путем вращения треугольника вокруг одного из его катетов. Прямые, исходящие из вершины конуса и пересекающие его основание, называются образующими. Если все образующие равны, то конус является прямым. В основании круглого конуса лежит круг. Перпендикуляр, опущенный на основание из вершины, является высотой конуса. У круглого прямого конуса высота совпадает с его осью. Ось – это прямая, соединяющая вершину с центром основания. Если горизонтальная секущая плоскость кругового конуса параллельна основанию, то его верхнее основание представляет собой круг.
2
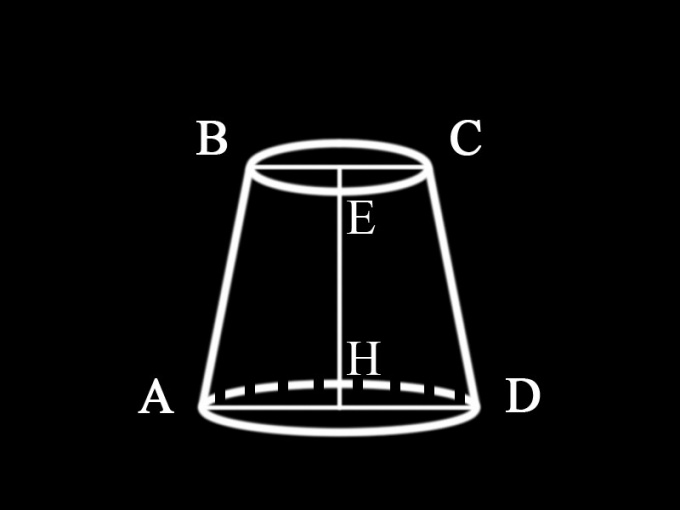
Поскольку в условии задачи не оговорено, какой именно конус дается в данном случае, можно сделать вывод, что это круглый прямой усеченный конус, горизонтальное сечение которого параллельно основанию. Его осевое сечение, т.е. вертикальная плоскость, которая проходит через ось круглого усеченного конуса, представляет собой равнобочную трапецию. Все осевые сечения круглого прямого конуса равны между собой. Следовательно, чтобы найти площадь осевого сечения, требуется найти площадь трапеции, основаниями которой являются диаметры оснований усеченного конуса, а боковые стороны – его образующие. Высота усеченного конуса является одновременно высотой трапеции.
3
Площадь трапеции определяется по формуле:S = ½(a+b) h, где S – площадь трапеции;a – величина нижнего основания трапеции;b – величина ее верхнего основания;h – высота трапеции.
4
Поскольку в условии не оговорено, какие именно величины даны, можно считать, что диаметры обеих оснований и высота усеченного конуса известны: AD = d1 – диаметр нижнего основания усеченного конуса;BC = d2 – диаметр его верхнего основания; EH = h1 – высота конуса.Таким образом, площадь осевого сечения усеченного конуса определяется: S1 = ½ (d1+d2) h1
Источники:
- площадь усеченного конуса