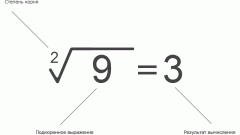Как возвести в корень число

Операция возведения числа в степень означает нахождение результата умножения его на себя такое количество раз, которое на единицу меньше указанного в показателе степени. Однако не всегда показатель степени является целым числом - иногда бывает необходимо, например, возвести число в степень, показатель которой представлен выражением, содержащим операцию извлечения корня.

Инструкция

1. Начните с вычисления или преобразования к более удобному виду показателя степени, который содержит операцию извлечения корня. Например, если по условиям задачи требуется число 25 возвести в степень, показателем которой является кубический корень из числа 81, то «извлеките» его и замените выражение (³√81) полученным значением (9).
2. Если полученное в результате извлечения корня на предыдущем шаге число является десятичной дробью, то попробуйте представить его в формате обыкновенной дроби. Например, если в условиях задачи из предыдущего шага показатель степени заменить на кубический корень из числа 3,375, то в результате его вычисления вы получите десятичную дробь 1,5. Ее можно записать в формате обыкновенной неправильной дроби 3/2. Возведение числа 25 в такую дробную степень означает, что из него надо извлечь корень второй степени, так как это число стоит в знаменателе показателя, а также возвести в третью степень, так как это число стоит в числителе (√25³). К сожалению не всякую десятичную дробь можно представить в форме обыкновенной дроби - чаще всего результатом извлечения корня является бесконечная дробь, то есть иррациональное число.
3. Воспользуйтесь калькулятором для вычисления как показателя, содержащего операцию извлечения корня, так и значения всего выражения. Если требуется только получить результат, опустив промежуточные преобразования, то можно обойтись одним лишь доступом в интернет - удобный в использовании калькулятор встроен, например, в поисковую систему Google. Скажем, если требуется число 3,87 возвести в степень, которая равна квадратному корню из числа 62,7, то введите в поле поискового запроса Google 3,87^sqrt(62,7). Результат вычисления (45049,6293) поисковик покажет сам, даже без нажатия на кнопку отправки запроса.