Вам понадобится
- Калькулятор, компьютер
Инструкция
1
Пусть имеется несколько чисел, характеризующих какие-либо однородные величины. Например, результаты измереений, взвешиваний, статистических наблюдений и т.п. Все представленные величины должны измеряться одной и той же единицей измерения. Чтобы найти среднее квадратичное отклонение, проделайте следующие действия.
Определите среднее арифметическое всех чисел: сложите все числа и разделите сумму на общее количество чисел.
Определите среднее арифметическое всех чисел: сложите все числа и разделите сумму на общее количество чисел.
2
Найдите отклонение каждого числа от его среднего значения: вычтите от каждого числа среднее арифметическое значение, посчитанное в предыдущем пункте.
3
Определите дисперсию (разброс) чисел: сложите квадраты найденных ранее отклонений и разделите полученную сумму на количество чисел.
4
Извлеките из дисперсии квадратный корень. Полученное число и будет средним квадратическим отклонением данного множества чисел.
5
Пример.
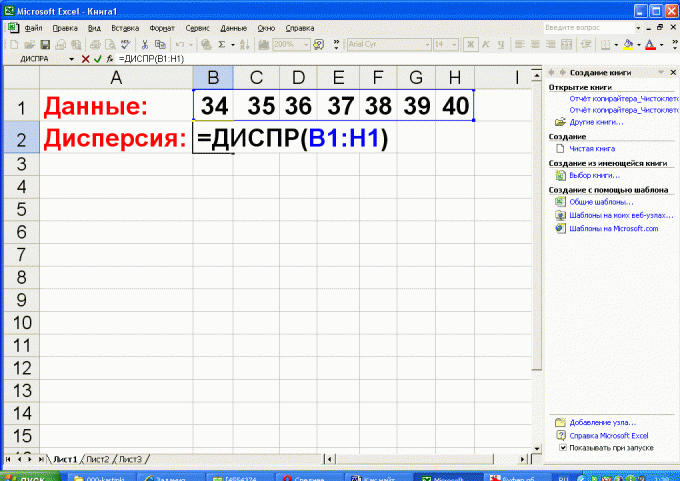
В палате лежат семь больных с температурой 34, 35, 36, 37, 38, 39 и 40 градусов Цельсия.
Требуется определить среднее квадратическое отклонение от средней температуры.
Решение:
• «средняя температура по палате»: (34+35+36+37+38+39+40)/7=37 ºС;
• отклонения температур от среднего (в данном случае нормального значения): 34-37, 35-37, 36-37, 37-37, 38-37, 39-37, 40-37, получается: -3, -2, -1, 0, 1, 2, 3 (ºС);
• дисперсия: ((-3)²+(-2)²+(-1)²+0²+1²+2²+3²)/7=(9+4+1+0+1+4+9)/7=4 (ºС²);
• среднее квадратическое отклонение: √4=2 (ºС);
Ответ: В среднем по палате температура – нормальная: 37 ºС, но среднее квадратическое отклонение температуры равняется 2 ºС, что указывает на серьезные проблемы у пациентов.
В палате лежат семь больных с температурой 34, 35, 36, 37, 38, 39 и 40 градусов Цельсия.
Требуется определить среднее квадратическое отклонение от средней температуры.
Решение:
• «средняя температура по палате»: (34+35+36+37+38+39+40)/7=37 ºС;
• отклонения температур от среднего (в данном случае нормального значения): 34-37, 35-37, 36-37, 37-37, 38-37, 39-37, 40-37, получается: -3, -2, -1, 0, 1, 2, 3 (ºС);
• дисперсия: ((-3)²+(-2)²+(-1)²+0²+1²+2²+3²)/7=(9+4+1+0+1+4+9)/7=4 (ºС²);
• среднее квадратическое отклонение: √4=2 (ºС);
Ответ: В среднем по палате температура – нормальная: 37 ºС, но среднее квадратическое отклонение температуры равняется 2 ºС, что указывает на серьезные проблемы у пациентов.
6
Если имеется возможность воспользоваться программой Excel, то вычисление дисперсии, а соответственно и среднего квадратического отклонения можно существенно упростить.
Для этого разместите данные измерений в один ряд (одну колонку) и воспользуйтесь статистической функцией ДИСПР. В качестве аргументов функции укажите диапазон ячеек таблицы, где размещены введенные числа.
Для этого разместите данные измерений в один ряд (одну колонку) и воспользуйтесь статистической функцией ДИСПР. В качестве аргументов функции укажите диапазон ячеек таблицы, где размещены введенные числа.
Источники:
- как вычислить среднее квадратическое