Инструкция
1
Если известна длина диаметра сферы (d), то для нахождения площади ее поверхности (S) возводите этот параметр в квадрат и умножайте на число Пи (π): S=π∗d². Например, если длина диаметра составляет два метра, то площадь сферы составит 3,14∗2²=12,56 квадратных метров.
2
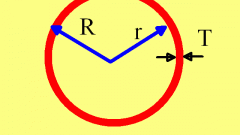
Если известна длина радиуса (r), то площадь поверхности сферы (S) будет составлять учетверенное произведение возведенного в квадрат радиуса на число Пи (π): S=4∗π∗r². Например, при длине радиуса сферы в три метра его площадь составит 4∗3,14∗3²=113,04 квадратных метров.
3
Если известен объем (V) пространства, ограниченного сферой, то сначала можно найти ее диаметр (d), а затем воспользоваться формулой, приведенной в первом шаге. Так как объем равен одной шестой части от произведения числа Пи на возведенную в куб длину диаметра сферы (V=π∗d³/6), то диаметр можно определить, как кубический корень из шести объемов, разделенных на число Пи: d=³√(6∗V/π). Подставив это значение в формулу из первого шага, получим: S=π∗(³√ (6∗V/π))². Например, при объеме ограниченного сферой пространства равном 500 кубометров вычисление ее площади будет выглядеть так: 3,14∗(³√(6∗500/3,14))² = 3,14∗(³√955,41)² = 3,14∗9,85² = 3,14∗97,02 = 304,64 квадратных метра.
4
Производить все эти расчеты в уме довольно затруднительно, поэтому придется воспользоваться каким либо из калькуляторов. Например, это может быть вычислитель, встроенный в поисковые системы Google или Nigma. Google отличается в лучшую сторону тем, что умеет самостоятельно определять порядок операций, а Nigma потребует от вас тщательно расставить все скобки. Для вычисления площади сферы по данным, например, из второго шага поисковый запрос, который надо ввести в Google, будет выглядеть так: «4*пи*3^2». А для наиболее сложного случая с вычислением кубического корня и возведением в квадрат из третьего шага запрос будет таким: «пи*(6*500/пи)^(2/3)».