Инструкция
1
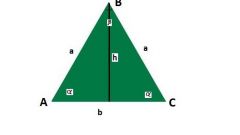
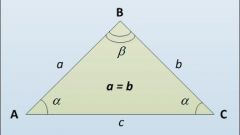
Если известна длина основания равнобедренного треугольника (A) и величина прилежащего к нему угла (угла между основанием и любой боковой стороной) (α), то вычислить длину каждой из боковых сторон (B) можно исходя из теоремы косинусов. Она будет равна частному от деления длины основания на удвоенное значение косинуса известного угла B=A/(2*cos(α)).
2
Длину стороны равнобедренного треугольника, являющейся его основанием (A), можно вычислить исходя из той же теоремы косинусов, если известны длина его боковой стороны (B) и угол между ней и основанием (α). Она будет равна удвоенному произведению известной стороны на косинус известного угла A=2*B*cos(α).
3
Другой способ нахождения длины основания равнобедренного треугольника можно использовать, если известна величина противолежащего ему угла (β) и длина боковой стороны (B) треугольника. Она будет равна удвоенному произведению длины боковой стороны на синус половины величины известного угла A=2*B*sin(β /2).
4
Аналогично можно вывести и формулу вычисления боковой стороны равнобедренного треугольника. Если известна длина основания (A) и величина угла между равными сторонами (β), то длина каждой из них (B) будет равна частному от деления длины основания на удвоенный синус половины величины известного угла B=A/(2*sin(β /2)).
5
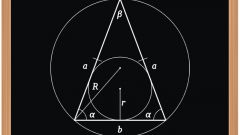
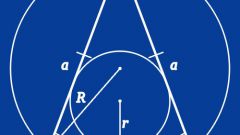
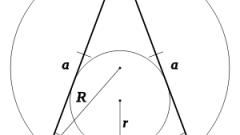
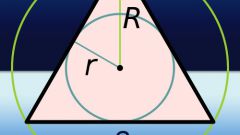
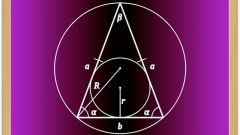
Если известен радиус описанной вокруг равнобедренного треугольника окружности (R), то длины его сторон можно рассчитать, зная величину одного из углов. Если известна величина угла между боковыми сторонами (β), то длина стороны, являющейся основанием (A), будет равна удвоенному произведению радиуса описанной окружности на синус этого угла A=2*R*sin(β).
6
Если известны радиус описанной окружности (R) и величина угла, прилегающего к основанию (α), то длина боковой стороны (B) будет равна удвоенному произведению длины основания на синус известного угла B=2*R*sin(α).