Вам понадобится
- - циркуль;
- - линейка;
- - карандаш.
Инструкция
1
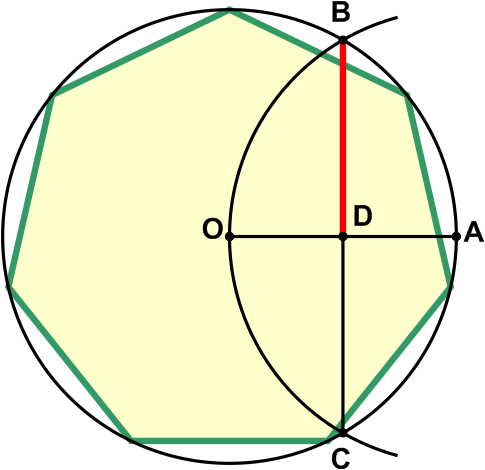
Чтобы начать построение, начертите произвольную окружность и обозначьте ее центр буквой О. Затем проведите радиус этой окружности в любом направлении. Точку пересечения радиуса с окружностью обозначьте буквой А. После этого переставьте циркуль в точку А и проведите окружность или дугу того же радиуса, что и у исходной окружности (ОА). Данная дуга пересечет исходную окружность в двух точках. Обозначьте их буквами В и С.
2
Соедините две полученные точки. При этом отрезок ВС пересечет радиус ОА. Точку их пересечения обозначьте буквой D. Образовавшиеся при этом отрезки ВD и DC будут равны между собой и каждый из них будет приблизительно равен стороне правильного семиугольника, который можно вписать в исходную окружность.
3
Отмерьте циркулем расстояние ВD (или DC) и, начиная с любой точки на окружности, отложите это расстояние шесть раз. Затем соедините все семь точек. Так вы получите семиугольник, который с небольшой погрешностью можно назвать правильным. Все его стороны и углы будут приблизительно равны.
4
Есть и другой способ построения правильного семиугольника. Для начала начертите произвольную окружность и проведите два взаимно перпендикулярных диаметра этой окружности. Назовите их АВ и СD. Далее один из диаметров (например, АВ) разделите на семь равных частей. Например, если длина вашего диаметра составляет 14 см, то длина каждой его части будет равна 2 см. В результате на данном диаметре должно появиться шесть отметок.
5
Затем переставьте циркуль в один из концов данного диаметра (например, В) и проведите из этой точки дугу, радиус которой будет равен диаметру исходной окружности (АВ). После этого продлите второй диаметр (СD) до пересечения с построенной дугой. Полученную точку обозначьте буквой Е.
6
Теперь из точки Е проведите прямые, проходящие только через четные или только через нечетные деления на диаметре АВ. Например, через второе, четвертое и шестое деления. Точки пересечения этих прямых с окружностью будут тремя из семи вершин вашего будущего многоугольника. Обозначьте их F, G и H. Четвертой вершиной будет точка А (в том случае, если вы проводили прямые через четные отметки) или точка В (если одна из прямых прошла через ближайшую к точке А отсечку).
7
Чтобы найти пятую, шестую и седьмую вершины, проведите из точек F, G и H прямые, строго перпендикулярные диаметру АВ. Те точки, в которых эти прямые пересекут противоположную сторону окружности, будут тремя искомыми вершинами. Для завершения построения вам нужно будет соединить все семь вершин.
Источники:
- Правильные многоугольники