Вам понадобится
- Оборудование Бумага Линейка Карандаш Транспортир Таблица синусов и косинусов Математические понятия: Свойства параллелограмма Свойства высоты треугольника Извлечение квадратного корня Теоремы синусов и косинусов
Инструкция
1
Постройте параллелограмм с заданными параметрами. В условиях должны быть заданы длины сторон параллелограмма и хотя бы один угол.
2
Вспомните, чему равна сумма квадратов диагоналей параллелограмма. Она равна удвоенной сумме квадратов его сторон, которые вам известны.
3
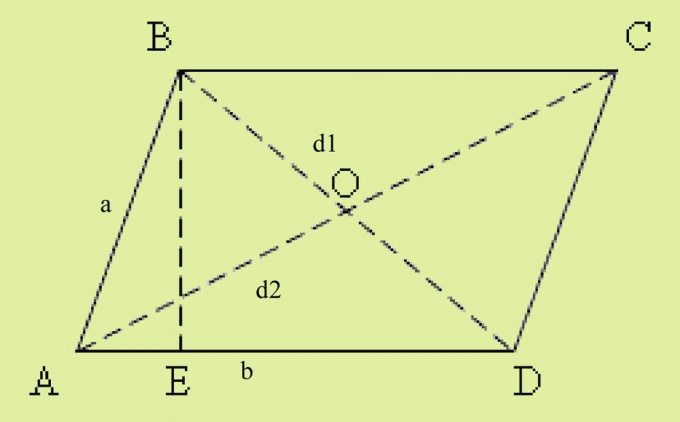
Обозначьте параллелограмм АBCD. Стороны параллелограмма обозначьте как a и b. Диагонали обозначьте как d1 и d2. Из угла В к стороне АD опустите высоту и обозначьте точку ее пересечения со стороной AD как Е. Внутри параллелограмма у вас получился прямоугольный треугольник АВЕ.
4
Найдите высоту BЕ. Вам известен угол А и гипотенуза АВ. AE = a*sinА
5
Вычислите длину отрезка АЕ. Он равен AE=a*cosA.
6
Вычислите отрезок ЕD, который равен разности стороны AD и отрезка AE.
7
Вычислите гипотенузу прямоугольного треугольника BED, которая одновременно является диагональю d1. Она будет равна квадратному корню из суммы квадратов сторон BE и ED.
8
Найдите квадрат второй диагонали. Он будет равняться удвоенной сумме квадратов сторон минус квадрат уже известной диагонали. Извлеките квадратный корень.
Обратите внимание
При построении параллелограмма строго следуйте заданным параметрам и пользуйтесь инструментами. При расчетах пользуйтесь таблицами синусов и косинусов.
Полезный совет
В прямоугольнике и квадрате диагонали равны. Квадрат диагонали прямоугольника равен сумме квадратов его сторон. В квадрате диагональ равна квадратному корню, извлеченному из удвоенного квадрата стороны. Диагонали ромба являются биссектрисами его углов.



