Инструкция
1
Если ФКП f(z) является аналитической в кольце 0
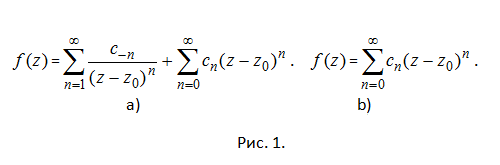
2
Если все коэффициенты главной части ряда Лорана равны нулю, то особая точка z0 называется устранимой особой точкой функции. Разложение в ряд Лорана в этом случае имеет вид (рис. 1b). Если главная часть ряда Лорана содержит конечное число k слагаемых, то особая точка z0 называется полюсом k-го порядка функции f(z). Если главная часть ряда Лорана содержит бесконечное число членов, то особая точка называется существенной особой точкой функции f(z).
3
Пример 1. Функция w=(z-2)/[((z-3)^2)z((z+1)^3)] имеет особые точки: z=3 – полюс второго порядка, z=0 полюс первого порядка, z=-1 - полюс третьего порядка. Обратите внимание, что все полюсы найдены путем нахождения корней уравнения ((z-3)^2)z((z+1)^3)=0.
4
Вычетом аналитической функции f(z) в выколотой окрестности точки z0 называют коэффициент с(-1) в разложении функции в ряд Лорана. Обозначается res[f(z), z0]. Учитывая формулу вычисления коэффициентов ряда Лорана, в частности, коэффициента с(-1) получается (см. рис. 2). Здесь γ – некоторый кусочно-гладкий замкнутый контур, ограничивающий односвязную область, содержащую точку z0 (например, окружность малого радиуса с центром в точке z0), и лежащую в кольце 0
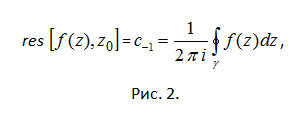
5
Итак, для нахождения вычета функции в изолированной особой точке следует либо разложить функцию в ряд Лорана и определить из этого разложения коэффициент с(-1), либо вычислить интеграл рисунка 2. Существуют и другие способы вычисления вычетов. Так, если точка z0 является полюсом порядка k функции f(z), то вычет в этой точке вычисляется по формуле (см. рис.3).
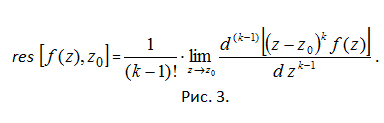
6
Если функция f(z)=φ(z)/ψ(z), где φ(z0)≠0, а ψ(z) имеет простой корень (кратности один) в z0, то ψ’(z0)≠0 и z0 является простым полюсом f(z). Тогда res[f(z),z0]= φ(z0)/ψ’(z0). Из этого правила достаточно наглядно вытекает вывод. Первое, что делается при нахождении особых точек – это знаменателя ψ(z).
Обратите внимание
Тренировка ума никогда не помещает. Особенно для тех, кто не так часто работает с цифрами, а уж тем более с корнями. Сложение и вычитание корней - хорошая разминка для скучающего ума. Нельзя складывать или вычитать выражения с разными подкоренными выражениями. Сложение корней требует соблюдение этого правила.
Полезный совет
Сложение и вычитание корней. Для сложения и вычитания корней соединяют их посредством знаков этих действий. Затем приводят корни к простейшей форме, и если между корнями окажутся подобные, то делают приведение. Это приведение состоит в том, что коэффициенты подобных членов, взятые со знаками соответствующих членов, заключают в скобки, а общий корень выводят за скобки множителем. Затем полученный общий коэффициент...