Инструкция
1
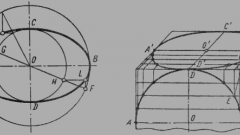
Задачи по нахождению линий пересечения позволяют решать широкий диапазон вопросов по конструированию технических деталей. В основу большинства решений входит построение линии с помощью вспомогательных плоскостей. Поскольку цилиндры являются поверхностями вращения с пересекающимися осями вращения, в качестве секущих плоскостей, как правило, используются сферы. Прежде чем построить линию пересечения, начертите два цилиндра с пересекающимися осями вращения. Центр оси вращения цилиндров является центром секущих сфер.
2
Определите крайние общие точки пересечения – самый большой и самый малый радиус. Максимальный радиус секущей сферы равняется расстоянию от центра оси вращения до самой далекой точки пересечения двух поверхностей. Проведите окружность сферы с максимальным радиусом и найдите точку её пересечения с цилиндрами – точку 1.
3
Минимальный радиус секущей сферы определяется с помощью двух нормалей K1 и K2. Поскольку сфера с наименьшим диаметром не пересекает сразу два цилиндра, в качестве минимального радиуса сферы принимается максимальная нормаль. Проведите окружность сферы с минимальным радиусом и найдите точку её пересечения с цилиндрами – точку 2.
4
Определите низшую точку пересечения цилиндров. Для чего постройте секущую сферу, которая пересекает первый цилиндр по окружности G, а второй цилиндр – по окружности D. Фронтальная проекция окружности G совпадает с проекцией оси вращения второго цилиндра. Точка пересечения двух окружностей – G и D – и является низшей точкой 3.
5
Постройте промежуточные точки пересечения двух цилиндров, используя метод построения произвольных сфер аналогично предыдущему действию. В результате вы получите две точки линии пересечения – 4 и 5.Соедините точки 1-5 плавной линии, тем самым образуя искомую линию пересечения для двух цилиндров.
Видео по теме
Источники:
- как построить линию пересечения двух цилиндров