Инструкция
1
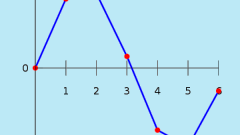
Представьте себе, что функция y=f(x) на отрезке [a,b] задана таблично (см. рис. 1). Данные таблицы чаще всего содержат опытные данные. Аргумент записывается в порядке возрастания (см. рис. 1). Здесь числа xi (i=1,2,…,n) называют точками согласования f(x) с g(x) или просто узлами.
2
Функция g(x) называется интерполирующей для f(x), а сама f(x) интерполируемой, если ее значения в узлах интерполяции xi (i=1,2,…,n) совпадают с заданными значениями функции f(x), то есть выполняются равенства: g(x1)=y1, g(x2)=y2,…, g(xn)=yn. (1)Итак, определяющее свойство – совпадение f(x) и g(x) в узлах (см. рис. 2).
3
В прочих точках может происходить что угодно. Так, если интерполирующая функция содержит синусоиды (косинусоиды), то отклонение от f(х) может быть весьма существенным, что маловероятно. Поэтому используются параболические (точнее, полиномиальные) интерполяции.
4
Для функции, заданной таблицей, осталось найти многочлен наименьшей степени Р(х) такой, чтобы выполнялись условия интерполяции (1): P(xi)=yi, i=1,2,…,n. Можно доказать, что степень такого многочлена не превышает (n-1). Для того чтобы избежать путаницы, далее задачу будем решать на конкретном примере четырехточечной задачи.
5
Пусть узловые точки: x1=-1, x2=1, x3=3, x4=5. y1=y(-1)=1, y2=y(1)=-5, y3=y(3)=29, y4=y(5)=245.В связи с изложенным выше, искомую интерполяцию следует искать в виде P3(x). Запишите искомый многочлен в виде P3(3)=ax^3+bx^2+cx+d и составьте систему уравнений (в числовой форме) a(xi)^3+b(xi)^2+c(xi)+d=yi (i=1, 2, 3, 4) относительно a, b, c, d (см. рис. 3).
6
Получилась система линейных уравнений. Решите ее любым известным вам способом (проще всего методом Гаусса).В данном примере ответ: a=3, b=-4, c=-6, d=2.Ответ. Интерполирующая функция (многочлен) g(x)=3x^3-4x^2-6x+2.
Видео по теме
Источники:
- Шипачев В.С. Высшая математика. Учеб. для вузов. – 3-е изд., стер. –М.: Высшая школа, 1996.-496 с.