Инструкция
1
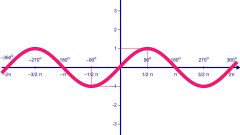
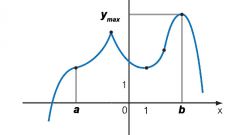
Функция y = F(x) является возрастающей на определенном интервале, если для любых точек x1 F(x2), где x1 всегда > x2 для любых точек на интервале.
2
Существуют достаточные признаки возрастания и убывания функции, которые вытекают из результата вычисления производной. Если производная функции положительна для любой точки интервала, то функция возрастает, если отрицательна – убывает.
3
Чтобы найти промежутки возрастания и убывания функции, нужно найти область ее определения, вычислить производную, решить неравенства вида F’(x) > 0 и F’(x)
Рассмотрим пример.
Найти промежутки возрастания и убывания функции для y = (3·x² + 2·x - 4)/x².
Найти промежутки возрастания и убывания функции для y = (3·x² + 2·x - 4)/x².
Решение.
1. Найдем область определения функции. Очевидно, что выражение, стоящее в знаменателе, должно всегда быть отличным от нуля. Поэтому точка 0 исключается из области определения: функция определена при x ∈ (-∞; 0)∪(0; +∞).
1. Найдем область определения функции. Очевидно, что выражение, стоящее в знаменателе, должно всегда быть отличным от нуля. Поэтому точка 0 исключается из области определения: функция определена при x ∈ (-∞; 0)∪(0; +∞).
2. Вычислим производную функции:
y’(x) = ((3·x² + 2·x - 4)’ ·x² – (3·x² + 2·x - 4) · (x²)’)/x^4 = ((6·x + 2) ·x² – (3·x² + 2·x - 4) ·2·x)/x^4 = (6·x³ + 2·x² – 6·x³ – 4·x² + 8·x)/x^4 = (8·x – 2·x²)/x^4 = 2· (4 - x)/x³.
y’(x) = ((3·x² + 2·x - 4)’ ·x² – (3·x² + 2·x - 4) · (x²)’)/x^4 = ((6·x + 2) ·x² – (3·x² + 2·x - 4) ·2·x)/x^4 = (6·x³ + 2·x² – 6·x³ – 4·x² + 8·x)/x^4 = (8·x – 2·x²)/x^4 = 2· (4 - x)/x³.
3. Решим неравенства y’ > 0 и y’ 0;
(4 - x)/x³
(4 - x)/x³
4. Левая часть неравенства имеет один действительный корень х = 4 и обращается в бесконечность при x = 0. Поэтому значение x = 4 включается и в промежуток возрастания функции, и в промежуток убывания, а точка 0 не включается никуда.
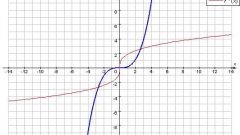
Итак, искомая функция возрастает на промежутке x ∈ (-∞; 0) ∪ [2; +∞) и убывает при x (0; 2].
Итак, искомая функция возрастает на промежутке x ∈ (-∞; 0) ∪ [2; +∞) и убывает при x (0; 2].
4
Рассмотрим пример.
Найти промежутки возрастания и убывания функции для y = (3·x² + 2·x - 4)/x².
Найти промежутки возрастания и убывания функции для y = (3·x² + 2·x - 4)/x².
5
Решение.
1. Найдем область определения функции. Очевидно, что выражение, стоящее в знаменателе, должно всегда быть отличным от нуля. Поэтому точка 0 исключается из области определения: функция определена при x ∈ (-∞; 0)∪(0; +∞).
1. Найдем область определения функции. Очевидно, что выражение, стоящее в знаменателе, должно всегда быть отличным от нуля. Поэтому точка 0 исключается из области определения: функция определена при x ∈ (-∞; 0)∪(0; +∞).
6
2. Вычислим производную функции:
y’(x) = ((3·x² + 2·x - 4)’ ·x² – (3·x² + 2·x - 4) · (x²)’)/x^4 = ((6·x + 2) ·x² – (3·x² + 2·x - 4) ·2·x)/x^4 = (6·x³ + 2·x² – 6·x³ – 4·x² + 8·x)/x^4 = (8·x – 2·x²)/x^4 = 2· (4 - x)/x³.
y’(x) = ((3·x² + 2·x - 4)’ ·x² – (3·x² + 2·x - 4) · (x²)’)/x^4 = ((6·x + 2) ·x² – (3·x² + 2·x - 4) ·2·x)/x^4 = (6·x³ + 2·x² – 6·x³ – 4·x² + 8·x)/x^4 = (8·x – 2·x²)/x^4 = 2· (4 - x)/x³.
7
3. Решим неравенства y’ > 0 и y’ 0;
(4 - x)/x³
(4 - x)/x³
4. Левая часть неравенства имеет один действительный корень х = 4 и обращается в бесконечность при x = 0. Поэтому значение x = 4 включается и в промежуток возрастания функции, и в промежуток убывания, а точка 0 не включается никуда.
Итак, искомая функция возрастает на промежутке x ∈ (-∞; 0) ∪ [2; +∞) и убывает при x (0; 2].
Итак, искомая функция возрастает на промежутке x ∈ (-∞; 0) ∪ [2; +∞) и убывает при x (0; 2].
8
4. Левая часть неравенства имеет один действительный корень х = 4 и обращается в бесконечность при x = 0. Поэтому значение x = 4 включается и в промежуток возрастания функции, и в промежуток убывания, а точка 0 не включается никуда.
Итак, искомая функция возрастает на промежутке x ∈ (-∞; 0) ∪ [2; +∞) и убывает при x (0; 2].
Итак, искомая функция возрастает на промежутке x ∈ (-∞; 0) ∪ [2; +∞) и убывает при x (0; 2].
Источники:
- как найти на функции промежутки убывания