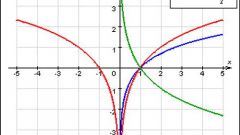
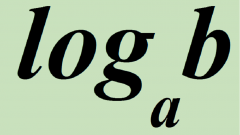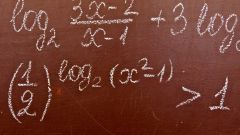Если основанием логарифма (то есть, тем числом, которое нужно возвести в степень) является 10, то логарифм называется «десятичным», и обозначается следующим образом: lg. Если же в роли основания выступает трансцендентное число e (примерно равное 2,718), то логарифм называется «натуральным», и обозначается ln. Для чего вообще нужны логарифмы? Какая от них практическая польза? Пожалуй, лучше всего ответил на эти вопросы знаменитый математик, физик и астроном Пьер-Симон Лаплас (1749-1827). По его мнению, изобретение такого показателя, как логарифм, словно удваивает жизнь астрономов, сокращая вычисления нескольких месяцев в труд нескольких дней. Некоторые на это могут ответить: мол, любителей тайн звездного неба сравнительно немного, а остальным-то людям что дают логарифмы? Говоря про астрономов, Лаплас имел в виду, прежде всего, тех, кто занимается сложными вычислениями. А изобретение логарифмов очень облегчило эту работу.В средние века математика в Европе, как и многие другие науки, практически не развивалась. Это происходило, прежде всего, из-за господства церкви, ревностно следившей, чтобы научное слово не расходилось со Священным Писанием. Но постепенно, с ростом числа университетов, а также с изобретением печатного станка математика стала возрождаться. Сильнейший толчок в развитии дисциплины дала эпоха Великих Географических Открытий. Морякам, отплывавшим на поиски новых земель, нужны были и точные карты, и астрономические таблицы для определения местоположения корабля. А для их составления требовались объединенные усилия астрономов-наблюдателей и математиков-вычислителей. Особая заслуга в этом объединении принадлежит гениальному ученому, Иоганну Кеплеру (1571 – 1630), который сделал фундаментальные открытия, работая над теорией движения небесных тел. Он же составил очень точные (по тем временам) астрономические таблицы. Но вычисления, необходимые для их составления, по-прежнему оставались очень сложными, они требовали колоссальных усилий и больших затрат времени. И так продолжалось до тех пор, пока не были изобретены логарифмы. Именно с их помощью стало возможным во много раз упростить и ускорить вычисления. Используя таблицы логарифмов, составленные знаменитым шотландским математиком Джоном Непером, можно без особых усилий перемножать числа, извлекать корни. Логарифм позволяет упростить умножение многозначных чисел путем сложения их логарифмов. Например, возьмем два числа, которые нужно умножить посредством логарифмов: 45,2 и 378. С помощью таблицы увидим, что по основанию 10 эти числа равны 1,6551 и 2,5775, то есть, 45,2 =10^1,6551 и 378=10^2,5775. Таким образом, 45,2*378=10^(1,6551+2,5775)=10^4,2326. Получили, что логарифм произведения чисел 45,2 и 378 равен 4,2326. Из таблицы логарифмов легко найти результат самого произведения.
Источники:
- Таблицы логарифмов