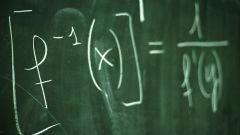Инструкция
1
Возьмите уравнения двух прямых, помня о том, что уравнение прямой в декартовой системе координат уравнение прямой выглядит как ах+ву+с=0, причем а, в, с – обычные числа, а х и у – координаты точек. Для примера найдите точки пересечения прямых 4х+3у-6=0 и 2х+у-4=0. Для этого найдите решение системы этих двух уравнений.
2
Для решения системы уравнений измените каждое из уравнений так, чтобы перед y стоял одинаковый коэффициент. Так как в одном уравнении коэффициент перед у равен 1, то просто умножьте это уравнение на число 3 (коэффициент перед у в другом уравнении). Для этого каждый элемент уравнения умножьте на 3: (2х*3)+(у*3)-(4*3)=(0*3) и получите обычное уравнение 6х+3у-12=0. Если бы коэффициенты перед у были отличны от единицы в обоих уравнениях, умножать надо было бы оба равенства.
3
Вычтите из одного уравнения другое. Для этого вычтите из левой части одного левую часть другого и точно также поступите с правой. Получите такое выражение: (4х+3у-6) - (6х+3у-12)=0-0. Так как перед скобкой стоит знак «-», все знаки в скобках поменяйте на противоположные. Получите такое выражение: 4х+3у-6 - 6х-3у+12=0. Упростите выражение и вы увидите, что переменная у исчезла. Новое уравнение выглядит так: -2х+6=0. Перенесите число 6 в другую часть уравнения, и из получившегося равенства -2х=-6 выразите х: х=(-6)/(-2). Таким образом, вы получили х=3.
4
Подставьте значение х=3 в любое уравнение, например, во второе и получите такое выражение: (2*3)+у-4=0. Упростите и выразите у: у=4-6=-2.
5
Запишите полученные значения х и у в виде координат точки (3;-2). Эти и будет решение задачи. Проверьте полученное значение методом подстановки в оба уравнения.
6
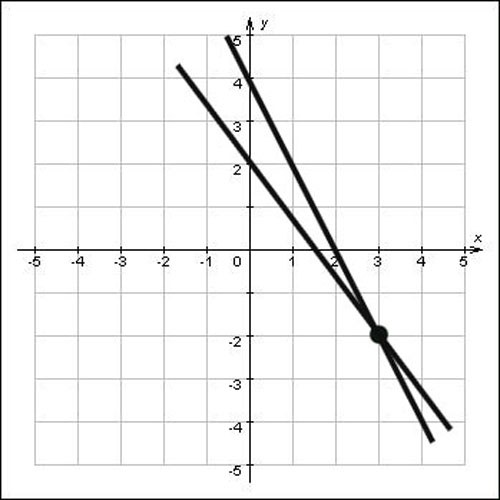
Если прямые не даны в виде уравнений, а даны просто на плоскости, найдите координаты точки пересечения графически. Для этого продлите прямые так, чтобы они пересеклись, затем опустите на оси ох и оу перпендикуляры. Пересечение перпендикуляров с осями ох и оу, будет координатами этой точки, посмотрите на рисунок и вы увидите, что координаты точки пересечения х=3 и у=-2, то есть точка (3;-2) и есть решение задачи.
Видео по теме