Вам понадобится
- Знать площадь трапеции, длины ее оснований, а также и длину средней линии.
Инструкция
1
Для того, чтобы вычислить площадь трапеции, необходимо воспользоваться следующей формулой:
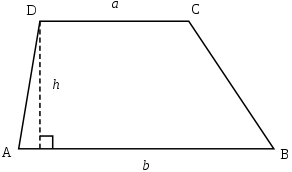
S = ((a+b)*h)/2, где a и b - основания трапеции, h - высота данной трапеции.
В том случае, если площадь и длины оснований известны, то найти высоту можно по формуле:
h = (2*S)/(a+b)
S = ((a+b)*h)/2, где a и b - основания трапеции, h - высота данной трапеции.
В том случае, если площадь и длины оснований известны, то найти высоту можно по формуле:
h = (2*S)/(a+b)
2
Если в трапеции известны ее площадь и длина средней линии, то найти ее высоту не составит труда:
S = m*h, где m - средняя линия, отсюда:
h = S/m.
S = m*h, где m - средняя линия, отсюда:
h = S/m.
3
Для того, чтобы оба способа были более понятными, можно привести пару примеров.
Пример 1: длина средней линии трапеции 10 см, ее площадь 100 см². Для нахождения высоты этой трапеции надо совершить действие:
h = 100/10 = 10 см
Ответ: высота данной трапеции 10 см
Пример 2: площадь трапеции 100 см², длины оснований равны 8 см и 12 см. Для нахождения высоты этой трапеции нужно выполнить действие:
h = (2*100)/(8+12) = 200/20 = 10 см
Ответ: высота данной трапеции 20 см
Пример 1: длина средней линии трапеции 10 см, ее площадь 100 см². Для нахождения высоты этой трапеции надо совершить действие:
h = 100/10 = 10 см
Ответ: высота данной трапеции 10 см
Пример 2: площадь трапеции 100 см², длины оснований равны 8 см и 12 см. Для нахождения высоты этой трапеции нужно выполнить действие:
h = (2*100)/(8+12) = 200/20 = 10 см
Ответ: высота данной трапеции 20 см
Обратите внимание
Существует несколько видов трапеций:
Равнобедренная трапеция - это такая трапеция, в которой боковые стороны равны между собой.
Прямоугольная трапеция - это трапеция, у которой один из внутренних углов равен 90 градусам.
Стоит отметить, что в прямоугольной трапеции высота совпадает с длиной стороны при прямом угле.
Вокруг трапеции можно описать окружность, или вписать ее внутрь данной фигуры. Вписать окружность можно лишь в том случае, если сумма оснований ее равна сумме противоположных сторон. Описать же окружность можно только вокруг равнобедренной трапеции.
Равнобедренная трапеция - это такая трапеция, в которой боковые стороны равны между собой.
Прямоугольная трапеция - это трапеция, у которой один из внутренних углов равен 90 градусам.
Стоит отметить, что в прямоугольной трапеции высота совпадает с длиной стороны при прямом угле.
Вокруг трапеции можно описать окружность, или вписать ее внутрь данной фигуры. Вписать окружность можно лишь в том случае, если сумма оснований ее равна сумме противоположных сторон. Описать же окружность можно только вокруг равнобедренной трапеции.
Полезный совет
Параллелограмм является частным случаем трапеции, ведь определение трапеции никак не противоречит определению параллелограмма. Параллелограмм - это четырехугольник, противоположные стороны которого параллельны между собой. У трапеции же в определении речь ведется лишь о паре его сторон. Поэтому любой параллелограмм является и трапецией. Обратное утверждение неверно.
Источники:
- как найти площадь трапеции формула