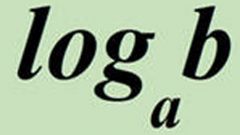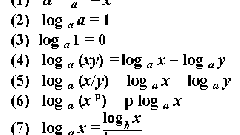Инструкция
1
Для вычисления логарифма с основанием равным 10 введите исходное число и нажмите на калькуляторе кнопку, отмеченную символом log. Если вы используете программный калькулятор, встроенный в операционную систему Windows, чтобы в наборе кнопок появилась и эта, его нужно переключить в «инженерный» интерфейс. Поэтому нажмите сочетание клавиш Alt + 2 или выберите пункт «Инженерный» в разделе «Вид» меню программы. Сразу после нажатия кнопки log вы увидите результат вычислений.
2
Операция нахождения натурального логарифма, основание которого равно математической константе e, производится так же просто - достаточно ввести исходное число и нажать кнопку калькулятора. В этом случае используйте кнопку, обозначенную символами ln.
3
Аналогичной функции для логарифмов с другими основаниями обычно нет в калькуляторах, но это не означает, что они не пригодны для таких операций. Основание можно изменить, если воспользоваться простой формулой - логарифм от некоторого числа (B) по какому-либо основанию (a) равен отношению логарифма этого же числа по другому основанию (x) к логарифму старого основания по новому: logₐB = logₓB/logₓa. Поскольку в любом калькуляторе предусмотрена работа с основанием, равным 10, используйте его в качестве «транзитного» параметра.
4
Описанный в предыдущем шаге алгоритм реализуйте таким способом: сначала введите основание исходного алгоритма и нажмите кнопку log. Полученное значение будет знаменателем дроби, пока поместите его в память калькулятора - нажмите клавишу M+. Введите число, из которого нужно извлечь логарифм, и снова нажмите кнопку log - так вы получите числитель дроби. Нажмите кнопку деления / и в качестве делителя используйте содержимое памяти - нажмите кнопку MR. Окончательный результат вычисления логарифма получите с помощью клавиши со знаком равенства.