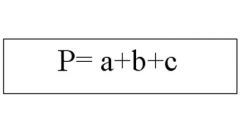Как найти периметр, если известна площадь и ширина

Периметр - это сумма всех сторон многоугольника. Если несколько сторон многоугольника имеют одинаковый размер, суммирование при вычислении периметра можно сочетать с умножением для ускорения расчета. Для правильных многоугольников применяются готовые формулы нахождения периметра.

Инструкция

1. Чтобы вычислить периметр при заданных площади и ширине многоугольника, нужно знать знать тип многоугольника. Параметры «длина» и «ширина» обычно применяются для характеристики прямоугольника. Прямоугольником называется четырехугольник с прямыми углами и попарно равными сторонами.
2. Определите длину прямоугольника. Для этого разделите заданную в условии площадь на ширину.
3. Периметр прямоугольника вычислите по формуле Р=2L+2S,где Р — искомый периметр; S — заданная в условии ширина; L — длина, вычисленная в п.2.
4. Частный случай прямоугольника — квадрат. Все четыре стороны квадрата равны. Поэтому для вычисления периметра достаточно знать размер одной стороны. Вычислите периметр квадрата по формуле Р=4S,где Р — искомый периметр; S — заданная в условии ширина.
5. Параллелограмм - тоже правильный многоугольник. Стороны в нем попарно равны и параллельны. Вычислить размер стороны параллелограмма по известной площади и другой стороне нельзя. Необходимо знать угол между сторонами параллелограмма. Заданных условий недостаточно для вычисления периметра параллелограмма.
6. Начертите произвольный параллелограмм. На сторону с известным по условию размером опустите высоту из вершины параллелограмма. При заданных ширине и площади высота параллелограмма — величина неизменная и равна частному от деления площади на ширину. Угол между сторонами параллелограмма по условию не задан. При изменении угла будет меняться размер неизвестной стороны параллелограмма. Таким образом задача имеет множество решений.