Вам понадобится
- Бумага, карандаш, циркуль, линейка, калькулятор, транспортир.
Инструкция
1
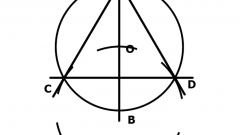
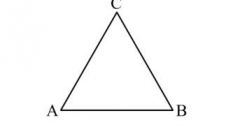
Если у вас есть возможность использовать при построении транспортир, начните с выбора произвольной точки на окружности, которая должна стать одной из вершин правильного треугольника. Обозначьте ее, например, буквой А.
2
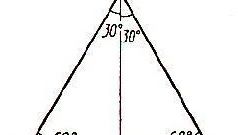
Начертите вспомогательный отрезок, соединив точку А с центром окружности. К этому отрезку приложите транспортир таким образом, чтобы нулевое деление совпало с центром круга, и поставьте вспомогательную точку у отметки 120°. Через эту точку проведите еще один вспомогательный отрезок с началом в центре круга и окончанием на пересечении с окружностью. Точку пересечения обозначьте буквой В - это вторая вершина вписанного треугольника.
3
Повторите предыдущий шаг, но транспортир прикладывайте ко второму вспомогательному отрезку, а точку пересечения с окружностью обозначьте буквой С. Больше транспортир не понадобится.
4
Соедините точки А и В, В и С, С и А. На этом построение правильного треугольника вписанного в окружность будет завершено.
5
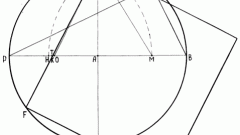
Если транспортира нет, но есть циркуль и калькулятор, то начните с вычисления длины стороны треугольника. Вы наверняка знаете, что ее можно выразить через радиус описанной окружности, умножив его на отношение тройки к квадратному корню из тройки, то есть примерно на 1,732050807568877. Округлите это число до нужной степени точности и умножьте на радиус круга.
6
Отметьте произвольную точку на окружности и обозначьте ее буквой А - это первая вершина правильного треугольника.
7
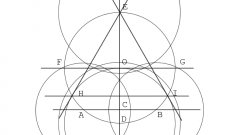
Отложите на циркуле найденную на пятом шаге длину стороны треугольника и начертите вспомогательный круг с центром в точке А. Точки пересечения двух окружностей обозначьте буквами В и С - это две другие вершины вписанного в круг правильного треугольника.
8
Соедините точки А и В, В и С, С и А и построение будет завершено.