Как отложить отрезок, равный данному

Отрезки называются равными только в том случае, если при наложении одного отрезка на другой их концы совпадут. Иными словами, равные отрезки имеют одинаковую длину. Метод построения с помощью циркуля является достаточно точным для того, чтобы отложить отрезок, равный данному.

Вам понадобится

• - линейка;
• - циркуль.

Инструкция

1. Постройте прямую a, на которой отложите произвольный отрезок AB. Согласно условию, в процессе решения задачи вам будет необходимо построить другой отрезок, равный ему. Пусть искомый отрезок будет обозначен как CD.
2. С помощью линейки постройте на листе бумаги другую случайную прямую b. Для удобства имеет смысл проводить ее так, чтобы на чертеже она была примерно той же длины, что и прямая a.
3. Нанесите на прямой b точку C. Можно выбрать какое угодно место, с точки зрения алгоритма решения задачи это не имеет значения, но из практических соображений лучше построить точку C так, чтобы на листе бумаги слева или справа от нее мог поместиться откладываемый отрезок.
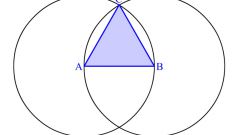
4. Измерьте циркулем расстояние между крайними точками искомого отрезка. Для этого поместите одну ножку циркуля в точку A, а другую в точку B.
5. После этого, не изменяя раствора циркуля, переставьте ножку из точки A в точку C. Другой ножкой, на которой закреплен кусочек грифеля, отметьте на прямой какую-нибудь точку. Это и будет искомая точка D.
6. Выделите получившийся отрезок CD более жирной линией. Задача решена, отрезок CD на прямой b будет равен отрезку AB на прямой a.