Инструкция
1
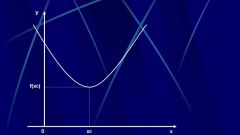
Предел функции (ПФ) в определенной точке, являющейся предельной для области определения данной конкретной функции обозначает величину, к коей она стремится при условии стремления ее аргумента (Х) к этой точке. Это наиболее часто используемое в теории математики понятие, которое обобщает понятие предела последовательности, потому что в ходе формирования понятий ПФ называли предел последовательности составляющих области значений определенной функции, состоящей из образов точек ряда элементов области ее определения, которые сходились к определенной точке. ПФ имеют различные варианты определения, основными из которых являются определения Коши и Гейне.
2
Вариант Коши: число L будет равно ПФ, для определенной функции F на интервале с точкой X, равной точке (т.) А , при Х стремящемся к А, если для каждого Е>0 есть D>0. При этому будут соблюдаться неравенства | f (x) - L|
Вариант определения ПФ по Гейне выражается так: F будет иметь предельное число L в определенной т. X, равной т. А, если для всех последовательностей, которые сходятся в точке А, последовательности будут сходиться к L. Эти определения не противоречат друг другу и являются эквивалентными.
Определение ПФ с использованием нескольких основных теорем:- Предельное значение суммы 2 функций, если Х стремится к А, будет равен сумме их предельных значений. - Предел произведения 2 функций, если Х стремится к А, будет соответствовать произведению их предельных значений. - Предел частного 2 функций, если Х стремится к А, будет равен частному их предельных значений, в том случае, если предел знаменателя в формуле не равен нулю.- Все элементарные функции являются непрерывными в точке, для которой они определены.- Предел определенной постоянной величины является самой постоянной величиной.
ПФ, являющийся одним из основополагающих понятий математического анализа, показывает изменение значения конкретной функции при бесконечно большом значении аргумента.
3
Вариант определения ПФ по Гейне выражается так: F будет иметь предельное число L в определенной т. X, равной т. А, если для всех последовательностей, которые сходятся в точке А, последовательности будут сходиться к L. Эти определения не противоречат друг другу и являются эквивалентными.
4
Определение ПФ с использованием нескольких основных теорем:- Предельное значение суммы 2 функций, если Х стремится к А, будет равен сумме их предельных значений. - Предел произведения 2 функций, если Х стремится к А, будет соответствовать произведению их предельных значений. - Предел частного 2 функций, если Х стремится к А, будет равен частному их предельных значений, в том случае, если предел знаменателя в формуле не равен нулю.- Все элементарные функции являются непрерывными в точке, для которой они определены.- Предел определенной постоянной величины является самой постоянной величиной.
5
ПФ, являющийся одним из основополагающих понятий математического анализа, показывает изменение значения конкретной функции при бесконечно большом значении аргумента.