Вам понадобится
- - калькулятор;
- - транспортир;
- - линейка.
Инструкция
1
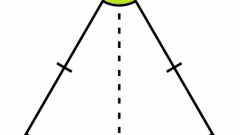
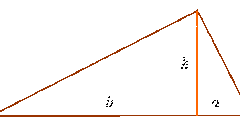
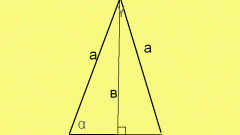
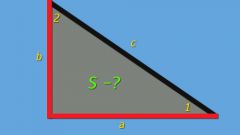
Чтобы найти площадь треугольника, умножьте длину его стороны на высоту (перпендикуляр, опущенный на эту сторону из противоположной вершины) и разделите полученное произведение на два. В виде формулы данное правило выглядит следующим образом:
S = ½ * а * h,
где:
S – площадь треугольника,
а – длина его стороны,
h – высота, опущенной на эту сторону.
Длина стороны и высота должны быть представлены в одинаковых единицах измерения. При этом площадь треугольника получится в соответствующих «квадратных» единицах.
S = ½ * а * h,
где:
S – площадь треугольника,
а – длина его стороны,
h – высота, опущенной на эту сторону.
Длина стороны и высота должны быть представлены в одинаковых единицах измерения. При этом площадь треугольника получится в соответствующих «квадратных» единицах.
2
Пример.
На одну из сторон разностороннего треугольника длиной 20 см, опущен перпендикуляр из противоположной вершины длиной 10 см.
Требуется определить площадь треугольника.
Решение.
S = ½ * 20 * 10 = 100 (см²).
На одну из сторон разностороннего треугольника длиной 20 см, опущен перпендикуляр из противоположной вершины длиной 10 см.
Требуется определить площадь треугольника.
Решение.
S = ½ * 20 * 10 = 100 (см²).
3
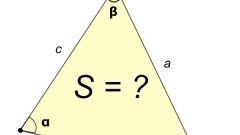
Если известны длины двух любых сторон разностороннего треугольника и угол между ними, то воспользуйтесь формулой:
S = ½ * а * b * sinγ,
где: а, b – длины двух произвольных сторон, а γ – величина угла между ними.
S = ½ * а * b * sinγ,
где: а, b – длины двух произвольных сторон, а γ – величина угла между ними.
4
На практике, например, при измерении площади земельных участков, использование вышеприведенных формул иногда бывает затруднительно, так как требует дополнительных построений и измерения углов.
Если вам известны длины всех трех сторон разностороннего треугольника, то воспользуйтесь формулой Герона:
S = √(p(p-a)(p-b)(p-c)),
где:
a, b, c – длины сторон треугольника,
р – полупериметр: p = (a+b+c)/2.
Если вам известны длины всех трех сторон разностороннего треугольника, то воспользуйтесь формулой Герона:
S = √(p(p-a)(p-b)(p-c)),
где:
a, b, c – длины сторон треугольника,
р – полупериметр: p = (a+b+c)/2.
5
Если кроме длин всех сторон известен радиус вписанной в треугольник окружности, то воспользуйтесь следующей компактной формулой:
S = p * r,
где: r – радиус вписанной окружности (р – полупериметр).
S = p * r,
где: r – радиус вписанной окружности (р – полупериметр).
6
Для вычисления площади разностороннего треугольника через радиус описанной окружности и длины его сторон, используйте формулу:
S = abc/4R,
где: R – радиус описанной окружности.
S = abc/4R,
где: R – радиус описанной окружности.
7
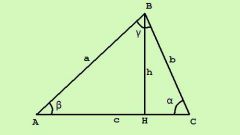
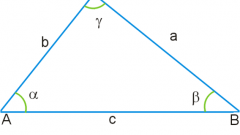
Если известна длина одной из сторон треугольника и величины трех углов (в принципе, достаточно двух – величина третьего вычисляется из равенства суммы трех углов треугольника - 180º), то воспользуйтесь формулой:
S = (a² * sinβ * sinγ)/2sinα,
где α – величина противолежащего стороне а угла;
β, γ – величины остальных двух углов треугольника.
S = (a² * sinβ * sinγ)/2sinα,
где α – величина противолежащего стороне а угла;
β, γ – величины остальных двух углов треугольника.