Инструкция
1
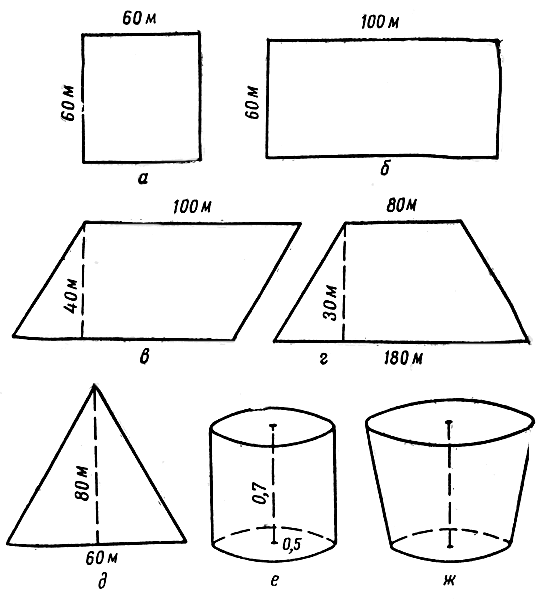
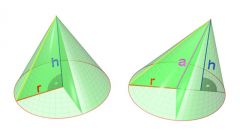
Перед нахождением высоты усеченного конуса ознакомьтесь с его определением. Усеченным конусом называется фигура, которая образована в результате перпендикулярного сечения плоскости обыкновенного конуса, при условии, что это сечение параллельно его основанию. Данная фигура имеет три характеристики:
- r1 - наибольший радиус;
- r2 - наименьший радиус;
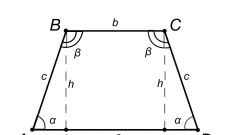
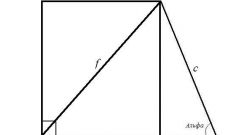
- h - высота.Кроме того, как и у обычного конуса, у усеченного имеется так называемая образующая, обозначаемая буквой l. Обратите внимание на внутреннее сечение конуса: оно представляет собой равнобедренную трапецию. Если ее вращать вокруг своей оси, получится усеченный конус с теми же параметрами. В данном случае, линия, делящая равнобедренную трапецию на две других, меньшего размера, совпадает с осью симметрии и с высотой конуса. Другая боковая сторона является образующей конуса.
- r1 - наибольший радиус;
- r2 - наименьший радиус;
- h - высота.Кроме того, как и у обычного конуса, у усеченного имеется так называемая образующая, обозначаемая буквой l. Обратите внимание на внутреннее сечение конуса: оно представляет собой равнобедренную трапецию. Если ее вращать вокруг своей оси, получится усеченный конус с теми же параметрами. В данном случае, линия, делящая равнобедренную трапецию на две других, меньшего размера, совпадает с осью симметрии и с высотой конуса. Другая боковая сторона является образующей конуса.
2
Зная радиусы конуса и его высоту, можно найти его объем. Он вычисляется следующим образом:V=1/3πh(r1^2+r1*r2+r2^2)Если известны два радиуса конуса, а также его объем, этого достаточно, чтобы найти и высоту фигуры:h=3V/π(r1^2+r1*r2+r2^2).В том случае, если в условии задачи даны диаметры окружностей, а не радиусы, данное выражение приобретает несколько иной вид:h=12V/π(d1^2+d1*d2+d2^2).
3
Зная образующую конуса и угол между ней и основанием данной фигуры, также можно найти ее высоту. Для этого нужно из другой вершины трапеции провести проекцию к большему радиусу, чтобы получился небольшой прямоугольный треугольник. Проекция будет равна высоте усеченного конуса. Если известна образующая l и угол, высота определите по следующей формуле:h=l*sinα.
4
Если по условию задачи известна лишь площадь сечения конуса, найти высоту невозможно, если неизвестны оба его радиуса.
Источники:
- как найти высоту конуса зная диаметр