Инструкция
1
Квадрат - равносторонний четырехугольник, в котором каждый угол равен 90°. Чтобы найти площадь (S) нужно умножить его длину (l) на ширину (b). Так как в этой фигуре длина и ширина равны, то достаточно знать одну из величин. Единицы измерения площади: см?, м?, км? и т.д.Например: длина одной стороны квадрата = 5 см. Нужно вычислить площадь. Найдите ее по формуле: S = l * b.
S = 5см * 5см.
S = 25см?.
Ответ: площадь квадрата со стороной 5 см равна 25 см?.
2
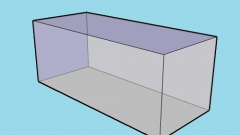
Куб - многогранник, в котором каждая грань – квадрат. Куб имеет двенадцать ребер, которые равны друг другу (т.е длина, ширина и высота одной грани – это длина (высота) ребра) и шесть одинаковых сторон. Чтобы найти объем куба, необходимо перемножить три его ребра (а). Единицы измерения объема: см?, дм?, м? и т.п.Например: длина ребра 5 см. Нужно найти объем куба. Рассчитайте по формуле:
V = а * а * а или V = a?.
V = 5см * 5см * 5 см.
V = 125 см?
Ответ: объем куба с длиной ребра 5 см равен 125 см?.
3
Если необходимо вычислить площадь всех сторон куба, то сначала найдите площадь одной стороны, а потом суммируйте площади всех шести сторон. Например: известно, что длина одной грани куба 5 см. Нужно найти площадь его поверхности. Решение имеет вид :
1. S = 5см*5 см = 25см?
2. ? = S+ S+ S+ S+ S+ S или S? =6*S
S?= 6*25см? = 150см?
Ответ: площадь поверхности куба с длиной ребра 5 см - 150см?Если требуется найти одну из геометрических характеристик, зная объем куба или площадь квадрата, то из значения объема извлекается кубический корень, а из значения площади - квадратный.
4
Периметр квадрата представляет собой сумму длин всех сторон. Т.е. нужно сложить значения четырех его длин.Например: длина квадрата 5 см. Вычислите периметр. Для вычисления периметра любого прямоугольника можно воспользоваться формулой: P = 2*(l+b).
Для квадрата формула имеет упрощенный вид: P = 4*l
P = 4*5см = 20см
Ответ: периметр квадрата длиной 5см – 20см.