Инструкция
1
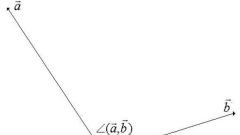
Прежде всего, вспомните, что вы знаете о прямой. Прямая – одно из самых главных основных понятий в геометрии. Это расстояние между двумя точками. Задается она на плоскости уравнением Ax + By = C. В данном уравнении А/В равно тангенсу угла наклона прямой, то есть угловому коэффициенту прямой. В задачах часто требуется найти угол между гранями фигуры.
2
3
Допустим, даны две прямые Ax+By=C и Dx+Ey=F. Для того чтобы найти угол между гранями этих прямых, необходимо сделать ряд следующих действий.
4
Выразите коэффициент угла наклона из этих уравнений прямых. Для первой прямой такой коэффициент будет равен A/B, а для второй - соответственно D/E. Чтобы было более наглядно, продемонстрируем на примерах. Так если уравнение прямой 4x+6y=20, соответственно, коэффициент угла будет равен 0,67. Если уравнение второй прямой -3x+5y=3, коэффициент угла наклона будет равен -0,6.
5
Найдите угол наклона каждой из прямых. Для этого необходимо посчитать арктангенс от полученного углового коэффициента. Так если брать на приведенном примере, arctg 0,67 будет равен 34 градуса, а arctg -0,6 - минус 31 градус. Таким образом, одна из прямых имеет положительный угловой коэффициент, а вторая - отрицательный. Угол между данными прямыми будет равняться сумме абсолютных величин этих углов. Если же оба коэффициента отрицательные или оба положительные, угол между гранями находится путем отнимания от большего меньшего.
6
Найдите угол между гранями. В нашем примере угол между гранями будет равен 65 градусов (|34| + |-31| = 34 + 31).
7
Следует знать, что период тригонометрической функции тангенс (tg) равен 180-ти градусам, а следовательно, угол наклона таких прямых по модулю не может превышать данное значение.
8
В случае когда угловые коэффициенты между собой равны, угол между гранями таких прямых будет равен нулю, так как прямые либо будут параллельны друг другу, либо будут совпадать.
Видео по теме
Источники:
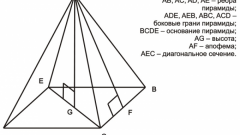
- Найдите угол между гранями правильного тетраэдра