Инструкция
1
Запишите функцию, исследование над которой необходимо провести, в виде y=y(x).
3
Упростите выражение.
4
Таким образом, вы получили одну и ту же функцию, записанную для аргументов "х" и "-х". Посмотрите на две эти записи.
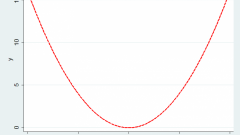
Если y(-x)=y(x), то это четная функция.
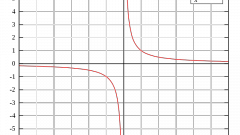
Если y(-x)=-y(x), то это нечетная функция.
Если же про функцию нельзя сказать, что y(-x)=y(x) или y(-x)=-y(x), то по свойству четности это функция общего вида. То есть, она не является ни четной, ни нечетной.
Если y(-x)=y(x), то это четная функция.
Если y(-x)=-y(x), то это нечетная функция.
Если же про функцию нельзя сказать, что y(-x)=y(x) или y(-x)=-y(x), то по свойству четности это функция общего вида. То есть, она не является ни четной, ни нечетной.
5
Запишите сделанные вами выводы. Теперь вы можете их использовать в построении графика функции или же в дальнейшем аналитическом исследовании свойств функции.
6
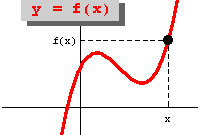
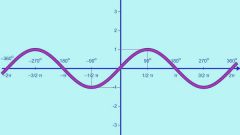
Говорить о четности и нечетности функции можно также и в том случае, когда уже задан график функции. Например, график послужил результатом физического эксперимента.
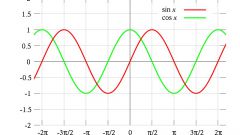
Если график функции симметричен относительно оси ординат, то y(x) - четная функция.
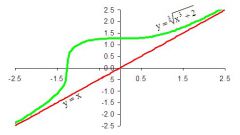
Если график функции симметричен относительно оси абсцисс, то x(y) - четная функция. x(y) - функция, обратная функции y(x).
Если график функции симметричен относительно начала координат (0,0), то y(x) - нечетная функция. Нечетной будет также обратная функция x(y).
Если график функции симметричен относительно оси ординат, то y(x) - четная функция.
Если график функции симметричен относительно оси абсцисс, то x(y) - четная функция. x(y) - функция, обратная функции y(x).
Если график функции симметричен относительно начала координат (0,0), то y(x) - нечетная функция. Нечетной будет также обратная функция x(y).
7
Важно помнить, что понятие о четности и нечетности функции имеет прямую связь с областью определения функции. Если, например, четная либо нечетная функция не существует при х=5, то она не существует и при х=-5, чего нельзя сказать про функцию общего вида. При установлении четности и нечетности обращайте внимание на область определения функции.
8
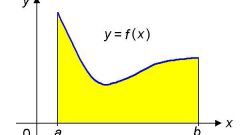
Исследование функции на четность и нечетность коррелирует с нахождением множества значений функции. Для нахождения множества значений четной функции достаточно рассмотреть половину функции, правее либо левее нуля. Если при x>0 четная функция y(x) принимает значения от А до В, то те же значения она будет принимать и при x<0.
Для нахождения множества значений, принимаемых нечетной функцией, тоже достаточно рассмотреть только одну часть функции. Если при x>0 нечетная функция y(x) принимает диапазон значений от А до В, то при x<0 она будет принимать симметричный диапазон значений от (-В) до (-А).
Для нахождения множества значений, принимаемых нечетной функцией, тоже достаточно рассмотреть только одну часть функции. Если при x>0 нечетная функция y(x) принимает диапазон значений от А до В, то при x<0 она будет принимать симметричный диапазон значений от (-В) до (-А).