Инструкция
1
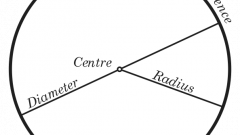
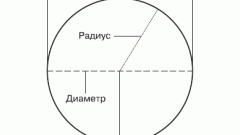
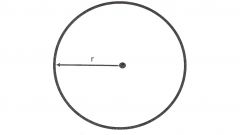
Для начала разберитесь в терминах и определениях, с которыми вам предстоит работать. Примите во внимание, что окружность - это это фигура, состоящая из всех точек плоскости, для каждой из которых отношение расстояний до двух данных точек равно данному числу, отличному от единицы. Радиус - это не только величина расстояния, но и отрезок, соединяющий центр окружности с одной из её точек. Длина окружности - это величина отрезка АВ, состоящего из точек А, В, а также всех точек плоскости, из которых отрезок АВ виден под прямым углом, отличное от диаметра. Пи - иррациональное число, то есть никогда не заканчивающееся и не являющееся периодическим и составляющее длину полуокружности, радиус которой равен единице, число Пи примерно равняется 3,14.
2
Итак, согласно первому способу, вычислить радиус окружности можно, если известен радиус окружности. Для этого умножьте длину радиуса на число Пи, примерно равное 3,14 и на цифру 2. Другими словами, стандартная формула вычисления радиуса окружности выглядит так: L = 2 х П х R, где L - длина окружности, П - число Пи (~3,141592654), R - радиус окружности. Следует отметить, что из данной формулы можно вычислить, чему равен радиус: R = L / (2 x П).
3
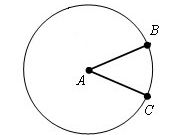
Существует более краткая формула для того, чтобы узнать радиан, то есть теоретически мы снова получаем формулу длины круга L = 2 х Пи х R, что свидетельствует о правильности данной формулы. Отсюда же следует, что число alpha также является постоянным значением и составляет 2 х Пи = 6,28. Таким образом, чтобы узнать длину окружности, умножьте радиус данной окружности на число 6,28.
Видео по теме
Источники:
- формула радиус окружности
- Как найти радиус окружности?