Как вычислить косинус угла

Косинус - одна из тригонометрических функций, которая применяется в решении геометрических и физических задач. Действия с векторами также редко обходятся без использования косинуса. Есть несколько способов вычисления косинуса угла от простейших арифметических действий до разложения в ряд Тейлора. Выбор способа зависит от необходимой точности значения косинуса.

Инструкция

1. Любому школьнику известны таблицы Брадиса. Он произвел множество кропотливых расчетов, но избавил математиков от трудоемкого подсчета значений основных тригонометрических функций для большого количества углов. До широкого распространения калькуляторов и вычислительных машин эти таблицы использовались практически всеми инженерами, математиками, физиками и студентами.
2. Вычислить косинус угла по таблице очень легко. Достаточно найти в столбце значений углов градусы угла, а затем идти по строке таблицы до пересечения с минутами угла. На рисунке показан фрагмент таблицы Брадиса. Видно, что значение косинуса для угла 72°30' составляет 0,3007. По таблицам Брадиса можно узнать значения функций с точностью до 0,0001, для большинства вычислений такая точность является вполне достаточной.
3. Изначально тригонометрические функции были связаны с прямоугольным треугольником и соотношением его сторон. Можно вспомнить об этом и применить известные соотношения, если угол является острым. Постройте прямоугольный треугольник с заданным углом. Для этого проведите два луча и опустите из какой-либо на одном из них перпендикуляр к другому. Теперь, если обозначить точки пересечения лучей буквами A, B и С, можно утверждать, что cos ∠BAC = CA/AB или отношению прилежащего к нему катета AC к гипотенузе AB. Точность этого метода невысока и сильно зависит от точности построений.
4. Для большей точности вычислений тригонометрические функции раскладывают в ряды Тейлора. Ряд Тейлора для косинуса смотрите на рисунке. Разложение в ряд позволяет вычислить косинус с любой точностью. Чем выше точность, тем больше членов ряда придется найти. Брадис в своих таблицах раскладывал косинус в ряд и находил первые несколько членов. Современные калькуляторы делают то же самое.
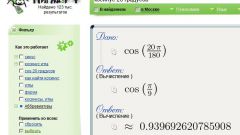
5. Попробуйте вручную вычислить значение косинуса для 72°30'. Для этого сначала переведите угол в радианы: 72°30' = 72,5°*π рад/180° = 1,2654 рад (заметьте, что значение числа π надо брать тоже достаточно точным, в данной формуле использовано π≈3,1416). Теперь подставьте это значение в ряд и вычислите несколько первых членов ряда: 1 - 1,2654^2/2 + 1,2654^4/24 - 1,2654^6/720 + 1,2654^8/40320 = 1 - 0,8006 + 0,1068 - 0,0057 + 0,0002 = 0,3006, где 720 = 6!, 40320 = 8!.
   Таким образом, cos 72°30' = cos 1,2654 рад ≈ 0,3006.