Инструкция
2
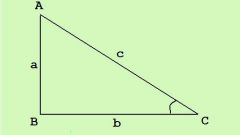
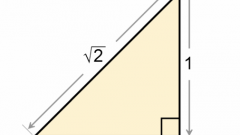
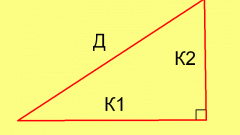
Найдите квадрат 2-й стороны. Возведем число 9 в квадрат, получим 81.
3
Сложите результаты 1-го и 2-го шага. Прибавим 225 к 81, получим 306.
4
Вычислите квадратный корень из результата 3-го шага. Корень из числа 306 примерно равен 17,49 сантиметров. Это и есть длина гипотенузы.
Обратите внимание
Если неизвестной величиной является один из катетов, то на 3-м шаге действуем иначе. Из квадрата гипотенузы вычитаем квадрат катета. Остальное не меняется. Например, была известна гипотенуза - 17,49 сантиметров. Также известен катет - 9 сантиметров. Найдем длину другого катета.
Число 17,49 в квадрате равно 305,9. Число 9 в квадрате равно 81. Вычитаем из числа 305,9 число 81, получаем 224,9. Вычисляем из этого числа корень, получаем 14,99 сантиметров - длина второго катета. Получилось чуть меньше 15 сантиметров, потому что 17,49 - мы изначально получили примерное, округленное значение.
Число 17,49 в квадрате равно 305,9. Число 9 в квадрате равно 81. Вычитаем из числа 305,9 число 81, получаем 224,9. Вычисляем из этого числа корень, получаем 14,99 сантиметров - длина второго катета. Получилось чуть меньше 15 сантиметров, потому что 17,49 - мы изначально получили примерное, округленное значение.
Полезный совет
Чтобы уверенно решать задачки по теореме Пифагора, потренируйтесь несколько раз. Решите штук 50 задач с разными прямоугольными треугольниками. И вы не забудете эту теорему никогда.
Источники:
- Решение прямоугольных треугольников
- известно 2 стороны треугольника
- Как по двум сторонам прямоугольного треугольника найти