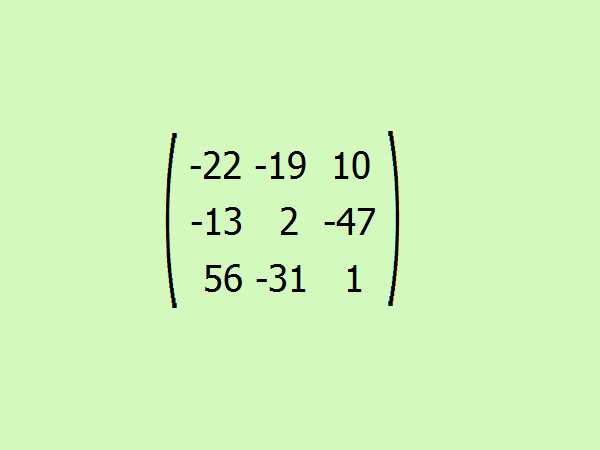Как найти присоединенную матрицу

Найти присоединенную матрицу можно только для квадратной исходной матрицы, поскольку метод расчета подразумевает предварительное транспонирование. Это одна из операций в матричной алгебре, итогом которой является замена столбцов соответствующими строками. Кроме того, необходимо определить алгебраические дополнения.

Инструкция

1. Основой матричной алгебры являются операции над матрицами и поиск их основных характеристик. Чтобы найти присоединенную матрицу необходимо выполнить транспонирование и сформировать на основе ее результата новую матрицу из соответствующих алгебраических дополнений.
2. Транспонирование квадратной матрицы – это запись ее элементов в другом порядке. Первый столбец меняется на первую строку, второй – на вторую и т.д. в общем виде это выглядит так (см. рисунок).
   
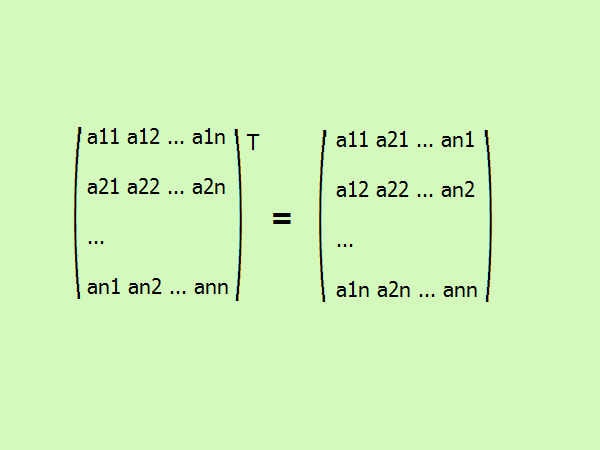
3. Второй этап нахождения присоединенной матрицы – поиск алгебраических дополнений. Эти числовые характеристики матричных элементов получаются путем вычисления миноров. Те, в свою очередь, являются определителями исходной матрицы порядка, меньшего на 1, и получаются вычеркиванием соответствующих строк и столбцов. Например, M11 = (a22•a33 – a23•a32). Алгебраическое дополнение отличается от минора коэффициентом, равным (-1) в степени суммы номеров элемента: A11 = (-1)^(1+1)• (a22•a33 – a23•a32).
4. Рассмотрите пример: найдите присоединенную матрицу к данной. Для удобства возьмем третий порядок. Это позволит быстрее понять алгоритм, не прибегая к тяжелым вычислениям, ведь для расчета определителей матрицы третьего порядка достаточно всего четырех элементов.
   
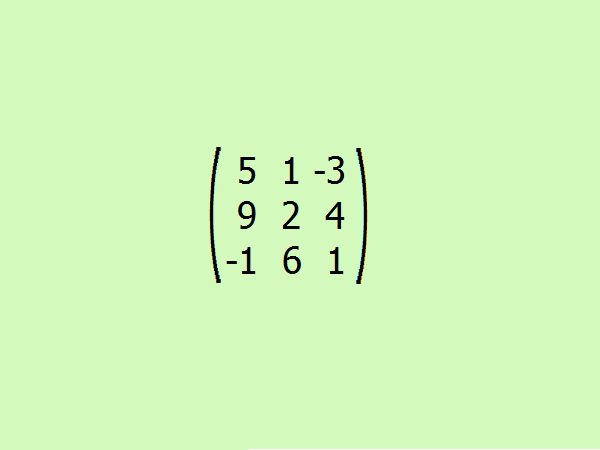
5. Проведите транспонирование заданной матрицы. Здесь требуется поменять местами первую строку на первый столбец, вторую – на второй и третью – на третий.
   
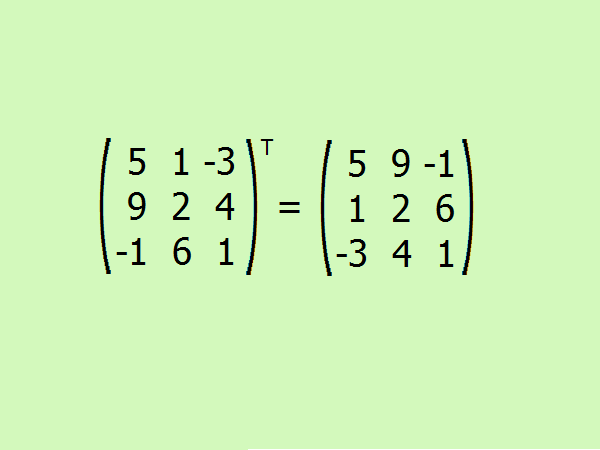
6. Запишите выражения для поиска алгебраических дополнений, всего их будет 9 по количеству элементов матрицы. Будьте внимательны со знаком, лучше воздержаться от расчетов в уме и расписать все подробно.
   
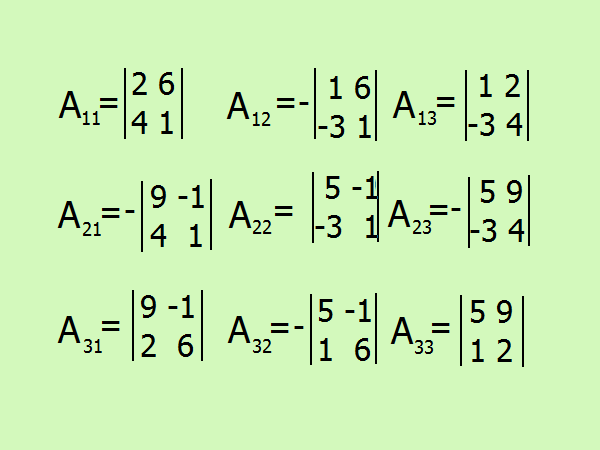
7. A11 = (-1)²•(2 -24) = -22;
   A12 = (-1)³•(1+ 18) = -19;
   A13 = (-1)^4•(4 + 6) = 10;
   A21 = (-1)³•(9 + 4) = -13;
   A22 = (-1)^4•(5 - 3) = 2;
   A23 = (-1)^5•(20 + 27);
   A31 = (-1)^4•(54 + 2) = 56;
   A32 = (-1)^5•(30 + 1) = -31;
   A33 = (-1)^6•(10 - 9) = 1.
8. Составьте итоговую присоединенную матрицу из получившихся алгебраических дополнений.