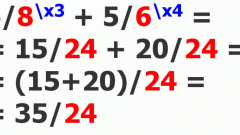Вам понадобится
  • - ручка;
  • - тетрадь;
  • - карандаш;
  • - циркуль.
Инструкция
1
Один из приемов сравнения обыкновенных дробей с разными числителями и знаменателями (без их приведения к общему знаменателю) – сравнение с половиной. К примеру, нужно узнать, что больше 5/9 или 3/7. Эти две дроби сравните с половиной, то есть 1/2.
2
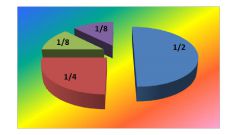
Для большей наглядности начертите окружность, в которой обозначьте 3/8, 1/2 и 5/9. Затем сравните 3/8 и 1/2 (3/8 меньше 1/2). Сравнив 5/9 с 1/2, вы обнаружите, что 5/9 больше 1/2.
3
С помощью этого приема несложно доказать, что 5/9 больше 3/8. Этот метод удобен, поскольку помогает визуально представить сравниваемые величины.
4
Второй способ сравнения обыкновенных дробей без их приведения к общему знаменателю – метод дополнения до единицы. К примеру, нужно определить, что больше 46/47 или 47/48. Получается, что для дополнения первой дроби до единицы нужно увеличить ее на 1/47, а второй – прибавить к ней 1/48.
5
Если сравнить 1/48 и 1/47 (к примеру, при помощи окружности), видно, что 1/48 меньше 1/47. Таким образом, 47/48 больше 46/47: для увеличения 47/48 до единицы понадобится дробь с меньшим значением, чем для увеличения 46/47.
6
Третий метод сравнения дробей основан на утверждении, что «неправильная дробь всегда больше правильной». Неправильной называется дробь, числитель которой больше знаменателя или равен ему. Следовательно, дробь, числитель которой меньше ее знаменателя, называется правильной.
7
К примеру, сравнить нужно 5/4 и 3/5. Учитывая тот факт, что 5/4 – это неправильная дробь, а 3/5 – правильная, несложно сделать вывод, что первая больше второй. Это утверждение справедливо, поскольку 5/4 больше единицы, а 3/5 меньше единицы.