Инструкция
1
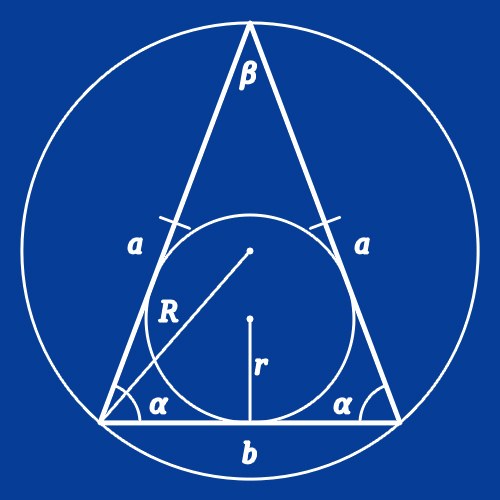
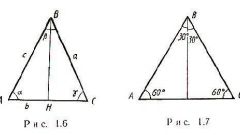
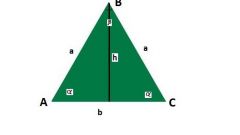
Для вычисления длины боковой стороны равнобедренного треугольника (b) по известной из условий длине основания (a) и величине прилегающего к нему угла (α) используйте теорему косинусов. Из нее вытекает, что вам следует разделить длину известной стороны на удвоенный косинус приведенного в условиях угла: b = a/(2*cos(α)).
2
Ту же теорему применяйте и для обратной операции - вычисления длины основания (a) по известной длине боковой стороны (b) и величине угла (α) между этими двумя сторонами. В этом случае теорема позволяет получить равенство, правая часть которого содержит удвоенное произведение длины известной стороны на косинус угла: a = 2*b*cos(α).
3
Если кроме длин боковых сторон (b) в условиях приведена величина угла между ними (β), для расчета длины основания (a) воспользуйтесь теоремой синусов. Из нее вытекает формула, согласно которой следует удвоенную длину боковой стороны умножить на синус половины известного угла: a = 2*b*sin(β /2).
4
Теорему синусов можно использовать и для нахождения длины боковой стороны (b) равнобедренного треугольника, если известна длина основания (a) и величина противолежащего ему угла (β). В этом случае удвойте синус половины известного угла и разделите на получившееся значение длину основания: b = a/(2*sin(β/2)).
5
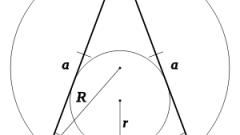
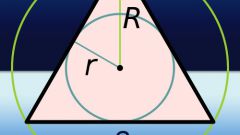
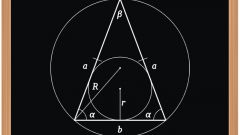
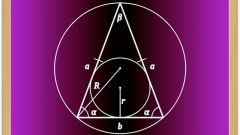
Если около равнобедренного треугольника описана окружность, радиус которой (R) известен, для вычисления длин сторон нужно знать величину угла в одной из вершин фигуры. Если в условиях приведена информация об угле между боковыми сторонами (β), вычисляйте длину основания (a) многоугольника удвоением произведения радиуса на значение синуса этого угла: a = 2*R*sin(β). Если же дана величина угла при основании (α), для нахождения длины боковой стороны (b) просто замените угол в этой формуле: b = 2*R*sin(α).
Видео по теме