Как найти коэффициент подобия треугольников

Подобные фигуры – это фигуры, одинаковые по форме, но разные по размеру.Треугольники являются подобными, если их углы равны, а стороны пропорциональны друг другу. Существуют также три признака, позволяющих определить подобие без соблюдения всех условий. Признак первый – у подобных треугольников два угла одного равны двум углам другого. Второй признак подобия треугольников - две стороны одного пропорциональны двум сторонам другого, а углы между этими сторонами у них равны. Третий признак подобия – это пропорциональность трех сторон одного трем сторонам другого.

Вам понадобится

• - ручка;
• - бумага для записей.

Инструкция

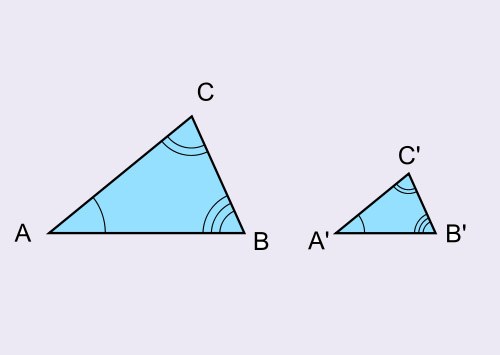
1. Коэффициент подобия выражает пропорциональность, это отношение длин сторон одного треугольника к сходственным сторонам другого: k = AB/A’B’= BC/B’C’ = AC/A’C’. Сходственные стороны в треугольниках находятся напротив равных углов. Коэффициент подобия можно найти разными способами.
   
2. Например, в задании даны подобные треугольники и приведены длины их сторон. Требуется найти коэффициент подобия. Поскольку треугольники подобны по условию, найдите их сходственные стороны. Для этого запишите длины сторон одного и другого по возрастанию. Найдите отношение сходственных сторон, которое будет коэффициентом подобия.
3. Вы можете вычислить коэффициент подобия треугольников, если вам известны их площади. Одно из свойств подобных треугольников гласит, что отношение их площадей равняется квадрату коэффициента подобия. Разделите значения площадей подобных треугольников одно на другое и извлеките квадратный корень из результата.
4. Отношения периметров, длин медиан, медиатрис, построенных к сходственным сторонам, равны коэффициенту подобия. Если разделить длину биссектрис или высот, проведенных из одинаковых углов, вы также получите коэффициент подобия. Воспользуйтесь этим свойством для нахождения коэффициента, если в условии задачи даны эти величины.
5. По теореме синусов для любого треугольника отношения сторон к синусам противолежащих углов равны диаметру описанной вокруг него окружности. Из этого вытекает, что у подобных треугольников отношение радиусов или диаметров описанных окружностей равно коэффициенту подобия. Если в задаче известны радиусы этих окружностей, или их можно вычислить из площадей кругов, найдите коэффициент подобия этим путем.
6. Используйте аналогичный путь для нахождения коэффициента, если у вас имеются вписанные в подобные треугольники окружности с известными радиусами.