Инструкция
1
Согласно условию на одном берегу реки находятся волк, коза и кочан капусты. Крестьянину необходимо перевести их на другой берег так, чтобы никто не пострадал. Ситуация осложняется тем, что поблизости нет моста, зато можно воспользоваться лодкой. Но в ней так мало места, что кроме самого крестьянина поместиться может кто-то один: волк, коза или капуста.
2
3
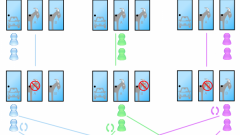
Когда она окажется на другом берегу, крестьянин поплывет обратно. Кого забрать следующим? Существует два одинаково верных решения: взять либо волка, либо капусту. Кого бы ни выбрал крестьянин, главное, причалив к другому берегу, высадить груз и отправиться обратно вместе с козой. Зачем? В первом случае, чтобы она не досталась на съедение волку, во втором – чтобы ей не удалось полакомиться капустой. Иными словами, если не взять козу в обратный путь, старик так и не перевезет груз в целости.
4
Когда лодка причалит к первому берегу, крестьянин должен высадить козу, взять волка/капусту, доставить груз к противоположному берегу, затем отправиться в завершающий рейс за козой. Таким образом, все трое останутся целы. Всего человеку придется переправиться через реку 7 раз.
5
Существует множество задач на переправу, требующих не только логического, но креативного мышления. Например, два человека стояли у реки. Оба они хотели попасть на другой берег и могли воспользоваться только одноместной лодкой. Как они смогли переправиться? Просто каждый находился с разных сторон реки. Первым перебрался на другую сторону тот, на чьем берегу находилась лодка.