Вам понадобится
- - две прямые на чертеже;
- - уравнения двух прямых.
Инструкция
1
2
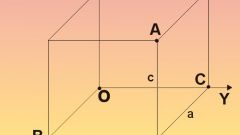
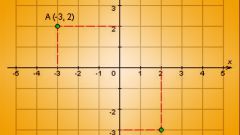
При помощи шкалы делений, отмеченных на оси, найдите значение х для этой точки. Если она находится на положительном направлении оси (справа от нулевой отметки), то ее значение будет положительным, в противном случае – отрицательным.
3
Точно также найдите ординату точки пересечения. Если проекция точки расположена выше нулевой отметки – она положительная, если ниже – отрицательная. Запишите координаты точки в виде (х, у) - это и есть решение задачи.
4
Если прямые заданы в виде формул у=kх+b, вы можете также решить задачу графическим способом: начертите прямые на координатной сетке и найдите решение описанным выше способом.
5
Попробуйте найти решение задачи, используя данные формулы. Для этого составьте из этих уравнений систему и решите ее. Если уравнения даны в виде у=kх+b, просто приравняйте обе части с х и найдите х. Затем подставьте значение х в одно из уравнений и найдите у.
6
Можно найти решение способом Крамера. В таком случае приведите уравнения к виду А1х+В1у+С1=0 и А2х+В2у+С2=0. Согласно формуле Крамера х=-(С1В2-С2В1)/(А1В2-А2В1), а у=-(А1C2-А2С1)/(А1В2-А2В1). Обратите внимание, если знаменатель равен нулю, то прямые параллельны или совпадают и, соответственно, не пересекаются.
7
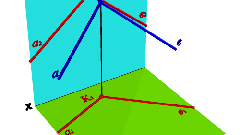
Если вам даны прямые в пространстве в каноническом виде, перед тем, как начать поиск решения, проверьте, не параллельны ли прямые. Для этого оцените коэффициенты перед t, если они пропорциональны, например, x=-1+3t, y=7+2t, z=2+t и x=-1+6t, y=-1+4t, z=-5+2t, то прямые параллельны. Кроме того, прямые могут скрещиваться, в этом случае система не будет иметь решения.
8
Если вы выяснили, что прямые пересекаются, найдите точку их пересечения. Сначала приравняйте переменные из разных прямых, условно заменив t на u для первой прямой и на v для второй прямой. Например, если вам даны прямые x=t-1, y=2t+1, z=t+2 и x=t+1, y=t+1, z=2t+8 вы получите выражения типа u-1=v+1, 2u+1=v+1, u+2=2v+8.
9
Выразите из одного уравнения u, подставьте в другое и найдите v (в данной задаче u=-2,v=-4). Теперь, чтобы найти точку пересечения, подставьте полученные значения вместо t (без разницы, в первое или второе уравнение) и получите координаты точки x=-3, y=-3, z=0.
Видео по теме
Источники:
- Нахождение точек пересечения прямых