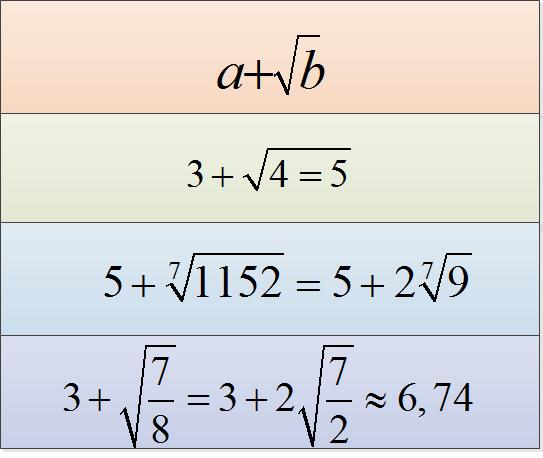Инструкция
1
Пусть задано выражения вида a + √b. Первое, что нужно сделать, - это определить, не является ли число b полным квадратом. Т.е. попробовать найти такое число c, что c^2 = b. В этом случае вы извлекаете квадратный корень из числа b, получаете число c и складываете его с числом a: a + √b = a + √(c^2) = a + с. Если вы имеете дело не с квадратным корнем, а с корнем n-й степени, то для полного извлечения числа b из под знака корня необходимо, чтобы это число было n-й степенью некоторого числа. Например, число 81 извлечется из под квадратного корня: √81 = 9. Также оно извлечется из под знака корня четвертой степени: (√4) 81 = 3.
2
Обратите внимание на следующие примеры.
• 7 + √25 = 7 + √(5^2) = 7 + 5 = 12. Здесь под знаком квадратного корня стоит число 25, которое является полным квадратом числа 5.
• 7 + (√3)27 = 7 + (√3) (3^3) = 7 + 3 = 10. Здесь был извлечен кубический корень из числа 27, которое является кубом числа 3.
• 7 + √(4/9) = 7 + √( (2/3)^2 ) = 7 + 2/3 = 23/3. Для извлечения корня из дроби необходимо извлечь корень из числителя и из знаменателя.
• 7 + √25 = 7 + √(5^2) = 7 + 5 = 12. Здесь под знаком квадратного корня стоит число 25, которое является полным квадратом числа 5.
• 7 + (√3)27 = 7 + (√3) (3^3) = 7 + 3 = 10. Здесь был извлечен кубический корень из числа 27, которое является кубом числа 3.
• 7 + √(4/9) = 7 + √( (2/3)^2 ) = 7 + 2/3 = 23/3. Для извлечения корня из дроби необходимо извлечь корень из числителя и из знаменателя.
3
Если число b под знаком корня не является полным квадратом, то попробуйте разложить его на множители и вынести множитель, являющийся полным квадратом, из под знака корня. Т.е. пусть число b имеет вид b = c^2 * d. Тогда √b = √(c^2 * d) = c * √d. Или же число b может содержать в себе квадраты двух чисел, т.е. b = c^2 * d^2 * e * f . Тогда √b = √(c^2 * d^2 * e * f) = c * d * √(e * f).
4
Примеры вынесения множителя из под знака корня:
• 3 + √18 = 3 + √(3^2 * 2) = 3 + 3√2 = 3 * (1 + √2).
• 3 + √(7 / 4) = 3 + √ (7 / 2^2) = 3 + √7 / 2 = (6 + √7) / 2. В данном примере был вынесен полный квадрат из знаменателя дроби.
• 3 + (√4)240 = 3 + (√4) (2^4 * 3 * 5) = 3 + 2 *(√4) 15. Здесь получилось вынести 2 в четвертой степени из под знака корня четвертой степени.
• 3 + √18 = 3 + √(3^2 * 2) = 3 + 3√2 = 3 * (1 + √2).
• 3 + √(7 / 4) = 3 + √ (7 / 2^2) = 3 + √7 / 2 = (6 + √7) / 2. В данном примере был вынесен полный квадрат из знаменателя дроби.
• 3 + (√4)240 = 3 + (√4) (2^4 * 3 * 5) = 3 + 2 *(√4) 15. Здесь получилось вынести 2 в четвертой степени из под знака корня четвертой степени.
5
И наконец, если вам необходимо получить приблизительный результат (в случае, если подкоренное выражение не является полным квадратом), воспользуйтесь калькулятором для вычисления значения корня. Например, 6 + √7 ≈ 6 + 2,6458 = 8,6458.
Полезный совет
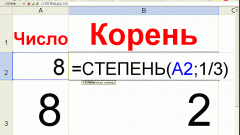
Для вычисления приблизительного значения корня на стандартном калькуляторе помните, что извлечь квадратный корень из числа равносильно возведению числа в степень 1/2. Аналогично извлечение кубического корня равносильно возведению числа в степень 1/3, корня четвертой степени – возведению числа в степень 1/4 и т.д.