Вам понадобится
  • калькулятор
Инструкция
1
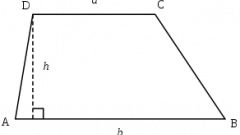
В задачах по геометрии, точнее по планиметрии и тригонометрии, иногда требуется найти высоту параллелограмма, исходя из заданных значений сторон, углов, диагоналей и т.п.

Чтобы найти высоту параллелограмма, зная его площадь и длину основания, необходимо воспользоваться правилом определения площади параллелограмма. Площадь параллелограмма, как известно, равняется произведению высоты на длину основания:

S=a*h, где:

S - площадь параллелограмма,

а - длина основания параллелограмма,

h - длина опущенной на сторону а высоты, (или на ее продолжение).

Отсюда получаем, что высота параллелограмма будет равняться площади, разделенной на длину основания:

h=S/a

Например,

дано: площадь параллелограмма равняется 50 кв.см., основание - 10 см.;

найти: высоту параллелограмма.

h=50/10=5 (см).
2
Так как высота параллелограмма, часть основания и прилежащая к основанию сторона образуют прямоугольный треугольник, то для нахождения высоты параллелограмма можно использовать некоторые соотношения сторон и углов прямоугольных треугольников.

Если известны прилежащая к высоте h (DE) сторона параллелограмма d (AD) и противоположный высоте угол A (BAD), то расчета высоты параллелограмма нужно умножить длину прилежащей стороны на синус противоположного угла:

h=d*sinA,

например, если d=10 см, а угол А=30 градусов, то

H=10*sin(30º)=10*1/2=5 (см).
3
Если в условиях задачи заданы длина прилежащей к высоте h (DE) стороне параллелограмма d (AD) и длина отсекаемой высотой части основания (АЕ), то высоту параллелограмма можно найти воспользовавшись теоремой Пифагора:

|AE|^2+|ED|^2=|AD|^2, откуда определяем:

h=|ED|=√(|AD|^2-|AE|^2),

т.е. высота параллелограмма равняется корню квадратному из разности квадратов длины прилежащей стороны и отсекаемой высотой части основания.

Например, если длина прилегающей стороны равняется 5 см., а длина отсекаемой части основания равна 3 см, то длина высоты будет:

h=√(5^2-3^2)=4 (см).
4
Если известны длина прилежащей к высоте диагональ (DВ) параллелограмма и длина отсекаемой высотой части основания (ВЕ), то высоту параллелограмма можно также найти воспользовавшись теоремой Пифагора:

|ВE|^2+|ED|^2=|ВD|^2, откуда определяем:

h=|ED|=√(|ВD|^2-|ВE|^2),

т.е. высота параллелограмма равняется корню квадратному из разности квадратов длины прилежащей диагонали и отсекаемой высотой (и диагональю) части основания.

Например, если длина прилегающей стороны равняется 5 см., а длина отсекаемой части основания равна 4 см, то длина высоты будет:

h=√(5^2-4^2)=3 (см).