Как найти векторное произведение векторов

Векторное произведение является одним из ключевых понятий векторного анализа. В физике различные величины находятся путем векторного произведения двух других величин. Осуществлять векторные произведения и преобразования на его основе нужно очень аккуратно, соблюдая основные правила.

Вам понадобится

• направления и длины двух векторов

Инструкция

1. Векторное произведение вектора a на вектор b в трехмерном пространстве записывается в виде c = [ab]. При этом вектор с должен удовлетворять ряду требований.
2. Длина вектора с равна произведению длин векторов a и b на синус угла между ними: |с| = |a||b|*sin(a^b).
   Вектор с ортогонален вектору a и ортогонален вектору b.
   Тройка векторов abc является правой.
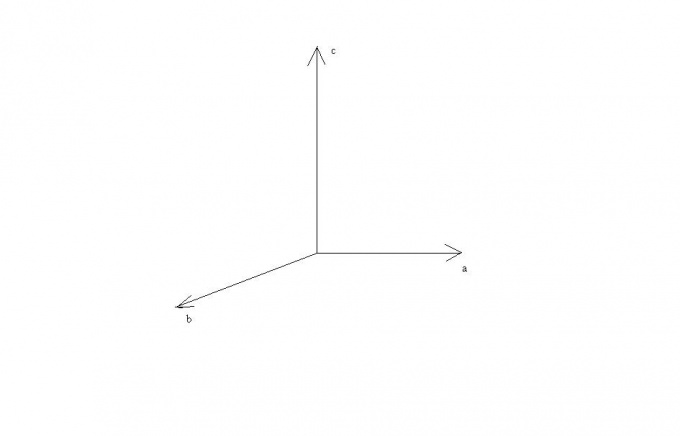
3. Из этих правил видно, что если векторы a и b параллельны или лежат на одной прямой, то их векторное произведение равно нулевому вектору, так как синус угла между ними равен нулю. В случае перпендикулярности векторов a и b векторы a,b и c будут перпендикулярны друг другу и их можно представить лежащими на осях прямоугольной декартовой системы координат.
4. Исходя из того, что тройка векторов abc является правой, направление вектора c можно найти по правилу правой руки. Сожмите руку в кулак, а затем направьте указательный палец вперед по направлению вектора a. Средний палец направьте по направлению вектора b. Тогда большой палец, направленный вверх, перпендикулярно указательному и среднему пальцу будет указывать направление вектора с.