Инструкция
1
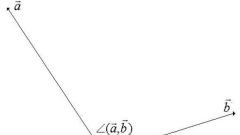
Угол между двумя ненулевыми векторами определяется с помощью вычисления скалярного произведения. По определению скалярное произведение равно произведению длин векторов на косинус угла между ними. С другой стороны, скалярное произведение для двух векторов a с координатами (x1; y1) и b с координатами (x2; y2) вычисляется по формуле: ab = x1x2 + y1y2. Из этих двух способов нахождения скалярного произведения легко найти угол между векторами.
2
Найдите длины или модули векторов. Для наших векторов a и b: |a| = (x1² + y1²)^1/2, |b| = (x2² + y2²)^1/2.
3
Найдите скалярное произведение векторов, перемножив их координаты попарно: ab = x1x2 + y1y2. Из определения скалярного произведения ab = |a|*|b|*cos α, где α - угол между векторами. Тогда получим, что x1x2 + y1y2 = |a|*|b|*cos α. Тогда cos α = (x1x2 + y1y2)/(|a|*|b|) = (x1x2 + y1y2)/((x1² + y1²)(x2² + y2²))^1/2.
4
Найдите угол α с помощью таблиц Брадиса.
5
В случае трехмерного пространства добавляется третья координата. Для векторов a (x1; y1; z1) и b (x2; y2; z2) формула для косинуса угла представлена на рисунке.
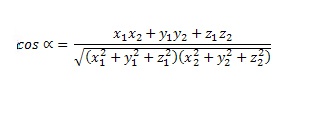
Видео по теме
Обратите внимание
Скалярное произведение - это скалярная характеристика длин векторов и угла между ними.