Вам понадобится
- - буман;
- - ручка.
Инструкция
1
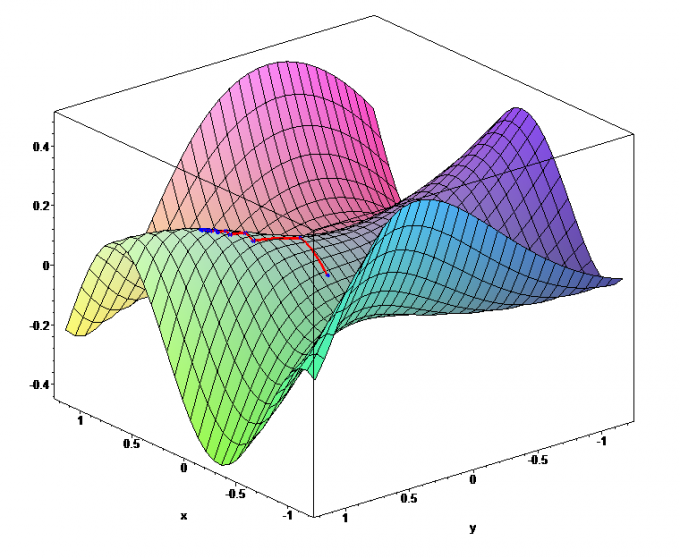
Пусть функция задается тремя аргументами u=f(x, y, z). Частную производную функции, на пример по х, определяют как производную по этому аргументу, полученную при фиксировании остальных аргументов. Для остальных аргументов аналогично. Обозначения частной производной записывается в виде: дf/дх = u’x …
2
Полный дифференциал будет равен du=(дf/дх)dx+ (дf/дy)dy+(дf/дz)dz.
Частные производные можно понимать, как производные по направлениям координатных осей. Поэтому возникает вопрос о нахождении производной по направлению заданного вектора s в точке M(x, y, z) (не забывайте, что направление s задает единичный вектор-орт s^o). При этом вектор-дифференциал аргументов {dx, dy, dz}={дscos(альфа), дsсоs(бета), дsсоs(гамма)}.
Частные производные можно понимать, как производные по направлениям координатных осей. Поэтому возникает вопрос о нахождении производной по направлению заданного вектора s в точке M(x, y, z) (не забывайте, что направление s задает единичный вектор-орт s^o). При этом вектор-дифференциал аргументов {dx, dy, dz}={дscos(альфа), дsсоs(бета), дsсоs(гамма)}.
3
Учитывая вид полного дифференциала du, можно сделать вывод, что производная по направле-нию s в точке М равна:
(дu/дs)|M=((дf/дх)|M)соs(альфа)+ ((дf/дy)|M) соs(бета) +((дf/дz)|M) соs(гамма).
Если s= s(sx,sy,sz), то направляющие косинусы {соs(альфа), соs(бета), соs(гамма)} вычисляются (см. рис.1а).
(дu/дs)|M=((дf/дх)|M)соs(альфа)+ ((дf/дy)|M) соs(бета) +((дf/дz)|M) соs(гамма).
Если s= s(sx,sy,sz), то направляющие косинусы {соs(альфа), соs(бета), соs(гамма)} вычисляются (см. рис.1а).
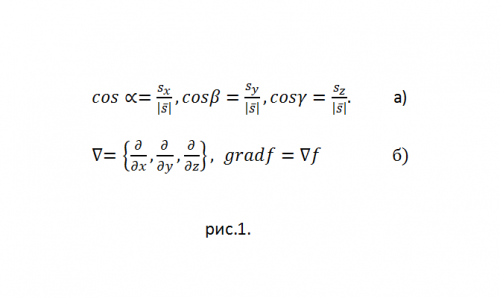
4
Определение производной по направлению, считая точку М переменной, можно переписать в виде скалярного произведения:
(дu/дs)=({дf/дх, дf/дy,дf/дz}, {соs(альфа), соs(бета), соs(гамма)})=(grad u, s^o).
Данное выражение будет справедливо для скалярного поля. Если рассматривается просто функ-ция, то gradf – это вектор, имеющий координаты, совпадающие с частными производными f(x, y, z).
gradf(x,y,z)={{дf/дх, дf/дy, дf/дz}=)=(дf/дх)i+(дf/дy)j +(дf/дz)k.
Здесь (i, j, k) – орты координатных осей в прямоугольной декартовой системе координат.
(дu/дs)=({дf/дх, дf/дy,дf/дz}, {соs(альфа), соs(бета), соs(гамма)})=(grad u, s^o).
Данное выражение будет справедливо для скалярного поля. Если рассматривается просто функ-ция, то gradf – это вектор, имеющий координаты, совпадающие с частными производными f(x, y, z).
gradf(x,y,z)={{дf/дх, дf/дy, дf/дz}=)=(дf/дх)i+(дf/дy)j +(дf/дz)k.
Здесь (i, j, k) – орты координатных осей в прямоугольной декартовой системе координат.
5
Если использовать дифференциальный вектор-оператор Гамильтона набла, то gradf можно записать, как умножение этого вектора-оператора на скаляр f (см. рис. 1б).
С точки зрения связи gradf c производной по направлению, равенство (gradf, s^o)=0 возможно, если эти векторы ортогональны. Поэтому gradf часто определяют, как направление быстрейшего изменения скалярного поля. А с точки зрения дифференциальных операций (gradf - одна из них), свойства gradf в точности повторяют свойства дифференцирования функций. В частности, если f=uv, то gradf=(vgradu+u gradv).
С точки зрения связи gradf c производной по направлению, равенство (gradf, s^o)=0 возможно, если эти векторы ортогональны. Поэтому gradf часто определяют, как направление быстрейшего изменения скалярного поля. А с точки зрения дифференциальных операций (gradf - одна из них), свойства gradf в точности повторяют свойства дифференцирования функций. В частности, если f=uv, то gradf=(vgradu+u gradv).
Видео по теме