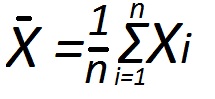Вам понадобится
- - математический справочник;
- - простой карандаш;
- - тетрадь;
- - ручка.
Инструкция
1
Графиком плотности нормального распределения называют нормальную кривую или кривую Гаусса. Обратите внимание на особенности, присущие нормальной кривой. Прежде всего ее функция определена на всей числовой прямой. Кроме того, при любых значения х функция данной кривой будет всегда положительной. Анализируя нормальную кривую, вы столкнетесь с тем, что ось ОХ будет для этого графика горизонтальной асимптотой (это объясняется тем, что при возрастании величины аргумента х уменьшается значение функции - оно стремится к нулю).
2
Найдите экстремум функции. Ввиду того, что при y’>0 x меньше m, а при y’
3
Чтобы найти точку перегиба графика нормальной кривой, определите вторую производную функции плотности. В точках x=m+s и x=m-s вторая производная будет равна нулю, а после перехода через данные точки ее знак будет изменен на противоположный.
4
Параметры и выражения нормального закона распределения представлены математическим ожиданием и среднеквадратичным отклонением случайной величины. Принимая во внимание эти данные, функция нормальной кривой определяется так, как показано на изображении.Ввиду этого, дисперсия и математическое ожидание характеризуют распределяемую случайную величину. Однако когда характер закона распределения не до конца понятен или неизвестен, для анализа данной функции дисперсии и математического ожидания будет недостаточно.
Видео по теме
Обратите внимание
Определение закона распределения начинается с классифицирования анализируемых непрерывных случайностей: уделите этому процессу особенное внимание.
Полезный совет
Если а=0 и s=1, то анализируемая кривая называется нормированной.
Источники:
- Нормальный закон распределения