Вам понадобится
- - простой карандаш;
- - тетрадь;
- - ручка.
Инструкция
1
Внимательно изучите условия задания: от того, насколько правильно вы его поймете, во многом зависит окончательный результат.
2
Для построения линии пересечения двух плоскостей найдите две общие точки данных плоскостей, через которые в дальнейшем будете проводить прямую линию. Обратите внимание на то, что заданная треугольником ABC плоскость может быть представлена прямыми линиями (АВ), (АС), (ВС). Точку, с которой прямая (АВ) пересекается с плоскостью a', обозначьте D, а с прямой (AС) назовите точкой F. Таким образом, отрезок (DF) определит линию пересечения этих двух плоскостей. Ввиду того, что a является горизонтально проецирующей плоскостью, проекция отрезка D1F1 будет совпадать со следом от плоскости aП1. Отсюда выходит, что вам осталось лишь построить недостающие проекции отрезка (DF) на плоскостях П2, а также П3.
3
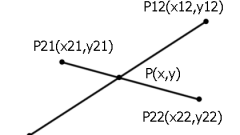
В том случае если даны плоскости общего положения, назовем их a(m,v) и b (ABC), построение линии между двумя плоскостями осуществите путем ввода двух вспомогательных секущих плоскостей (y и в). После этого найдите линии пересечения данных плоскостей с теми плоскостями, которые заданы по условию задания. Пусть плоскость y будет пересекаться с плоскостью a по прямой (12), а с плоскостью b - по прямой (34). Прямые (12) и (34) имеют общую точку пересечения Р, которая одновременно принадлежит трем плоскостям a, b и y. Предположите, что плоскость в пересекается с плоскостью a по прямой (56), а с плоскостью b - по прямой (78). Точка пересечения прямых (56) и (78) – К (она принадлежит трем плоскостям a, b и y, а также линиям пересечения плоскостей a и b). Ввиду этого, РК и будет линией пересечения плоскостей a и b.
Обратите внимание
Не запутайтесь с названием плоскостей!
Полезный совет
Выделяют следующие схемы построения линии пересечения поверхностей: секущие сферы и секущие плоскости.
Источники:
- Пересекающиеся плоскости
- пересечение прямой линии с плоскостью