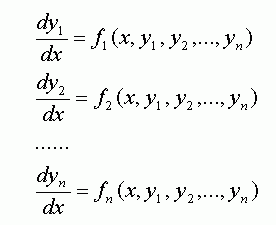Начнем с определения дифференциального уравнения. Итак, дифференциальное уравнение - это уравнение, которое связывает значение производной функции с самой функцией, значениями независимой переменной и некоторыми числами (параметрами).
Самая распространенная область, в которой применяются дифференциальные уравнения - математическое описание природных явлений. Также их применяют при решении задач, где невозможно установить прямую связь между некоторыми значениями, описывающими какой-либо процесс. Такие задачи возникают в биологии, физике, экономике.
Первой содержательной математической моделью, описывающей биологические сообщества была модель Лотки — Вольтерры. Она описывает популяцию, состоящую из двух взаимодействующих видов. Первый из них, именуемый хищниками, при отсутствии второго вымирает по закону x′ = –ax (a > 0), а второй — жертвы — при отсутствии хищников неограниченно размножается в соответствии с законом Мальтуса. Взаимодействие двух этих видов моделируется так. Жертвы вымирают со скоростью, равной числу встреч хищников и жертв, которое в данной модели предполагается пропорциональным численности обеих популяций, т. е. равной dxy (d > 0). Поэтому y′ = by – dxy. Хищники же размножаются со скоростью, пропорциональной числу съеденных жертв: x′ = –ax + cxy (c > 0). Система уравнений
x′ = –ax + cxy, (1)
y′ = by – dxy, (2)
описывающая такую популяцию хищник — жертва и называется системой (или моделью) Лотки — Вольтерры.
Второй закон Ньютона можно записать в форме дифференциального уравнения
m((d^2)x)/(dt^2) = F(x,t),
где m — масса тела, x — его координата, F(x, t) — сила, действующая на тело с координатой x в момент времени t. Его решением является траектория движения тела под действием указанной силы.
Модель естественного роста выпуска
Будем полагать, что некоторая продукция продается по фиксированной цене Р. Обозначим через Q(t) количество продукции, реализованной на момент времени t; тогда на этот момент времени получен доход, равный PQ(t). Пусть часть указанного дохода расходуется на инвестиции в производство реализуемой продукции, т.е.
I(t)=mPQ(t), (1)
где m — норма инвестиции — постоянное число, причем 0
Самая распространенная область, в которой применяются дифференциальные уравнения - математическое описание природных явлений. Также их применяют при решении задач, где невозможно установить прямую связь между некоторыми значениями, описывающими какой-либо процесс. Такие задачи возникают в биологии, физике, экономике.
В биологии:
Первой содержательной математической моделью, описывающей биологические сообщества была модель Лотки — Вольтерры. Она описывает популяцию, состоящую из двух взаимодействующих видов. Первый из них, именуемый хищниками, при отсутствии второго вымирает по закону x′ = –ax (a > 0), а второй — жертвы — при отсутствии хищников неограниченно размножается в соответствии с законом Мальтуса. Взаимодействие двух этих видов моделируется так. Жертвы вымирают со скоростью, равной числу встреч хищников и жертв, которое в данной модели предполагается пропорциональным численности обеих популяций, т. е. равной dxy (d > 0). Поэтому y′ = by – dxy. Хищники же размножаются со скоростью, пропорциональной числу съеденных жертв: x′ = –ax + cxy (c > 0). Система уравнений
x′ = –ax + cxy, (1)
y′ = by – dxy, (2)
описывающая такую популяцию хищник — жертва и называется системой (или моделью) Лотки — Вольтерры.
В физике:
Второй закон Ньютона можно записать в форме дифференциального уравнения
m((d^2)x)/(dt^2) = F(x,t),
где m — масса тела, x — его координата, F(x, t) — сила, действующая на тело с координатой x в момент времени t. Его решением является траектория движения тела под действием указанной силы.
В экономике:
Модель естественного роста выпуска
Будем полагать, что некоторая продукция продается по фиксированной цене Р. Обозначим через Q(t) количество продукции, реализованной на момент времени t; тогда на этот момент времени получен доход, равный PQ(t). Пусть часть указанного дохода расходуется на инвестиции в производство реализуемой продукции, т.е.
I(t)=mPQ(t), (1)
где m — норма инвестиции — постоянное число, причем 0
Источники:
- Дифференциальные уравнения - общая информация и сфера применения