Вам понадобится
- - математический справочник.
Инструкция
1
Обратите внимание на то, что периодическая функция не всегда имеет наименьший положительный период. Так, к примеру, в качестве периода постоянной функции может быть абсолютно любое число, а значит, у нее может и не быть наименьшего положительного периода. Встречаются также и непостоянные периодические функции, у которых нет наименьшего положительного периода. Однако в большинстве случаев наименьший положительный период у периодических функций все же есть.
2
Наименьший период синуса равен 2?. Рассмотрите доказательство этого на примере функции y=sin(x). Пусть T будет произвольным периодом синуса, в таком случае sin(a+T)=sin(a) при любом значении a. Если a=?/2, получается, что sin(T+?/2)=sin(?/2)=1. Однако sin(x)=1 лишь в том случае, когда x=?/2+2?n, где n представляет собой целое число. Отсюда следует, что T=2?n, а значит, наименьшим положительным значением 2?n является 2?.
3
Наименьший положительный период косинуса тоже равен 2?. Рассмотрите доказательство этого на примере функции y=cos(x). Если T будет произвольным периодом косинуса, то cos(a+T)=cos(a). В том случае если a=0, cos(T)=cos(0)=1. Ввиду этого, наименьшим положительным значением T, при котором cos(x)=1, есть 2?.
4
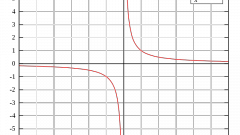
Учитывая тот факт, что 2? – период синуса и косинуса, это же значение будет и периодом котангенса, а также тангенса, однако не минимальным, поскольку, как известно, наименьший положительный период тангенса и котангенса равен ?. Убедиться в этом сможете, рассмотрев следующий пример: точки, соответствующие числам (х) и (х+?) на тригонометрической окружности, имеют диаметрально противоположное расположение. Расстояние от точки (х) до точки (х+2?) соответствует половине окружности. По определению тангенса и котангенса tg(x+?)=tgx, а ctg(x+?)=ctgx, а значит, наименьший положительный период котангенса и тангенса равен ?.
Обратите внимание
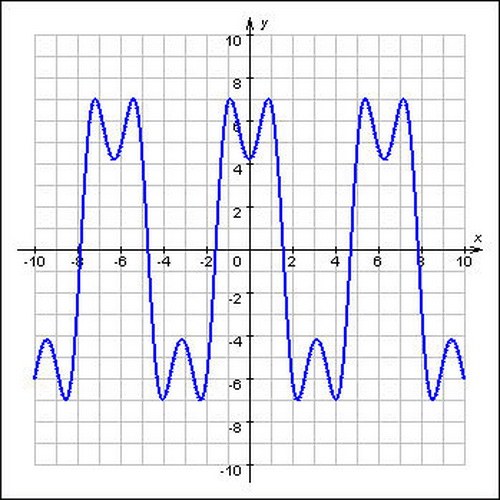
Не путайте функции y=cos(x) и y=sin(x) - имея одинаковый период, эти функции изображаются по-разному.
Полезный совет
Для большей наглядности изобразите тригонометрическую функцию, у которой рассчитывается наименьший положительный период.
Источники:
- Справочник по математике, школьная математика, высшая математика