Инструкция
1
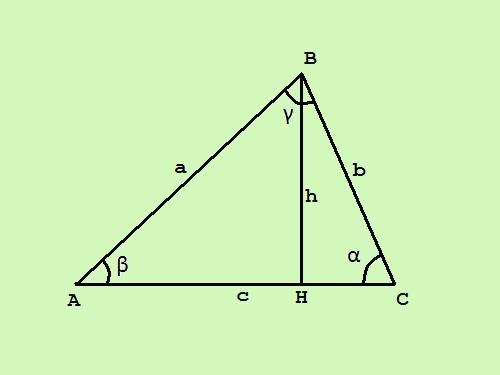
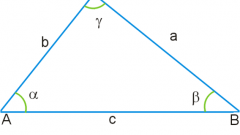
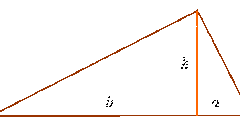
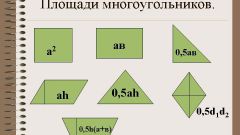
Основная формула площади произвольного треугольника ABC вычисляется следующим образом: S = ?*c*h, где c – основание треугольника, h – высота, проведенная к этому основанию.
2
Формула расчета площади через произведение сторон и sin угла между ними:S = ?*a*b*sin?.
3
4
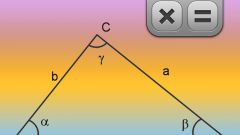
Пусть вокруг треугольника описана окружность радиуса R. Формула площади треугольника через радиус описанной окружности и длины сторон треугольника:S = (a*b*c)/(4*R).Формула площади треугольника через радиус описанной окружности и углы треугольника:S = 2*R^2*sin?*sin?*sin?.
5
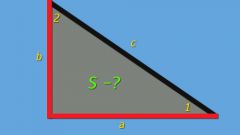
Существует формула Герона для площади треугольника, названная по имени древнегреческого математика Герона Александрийского, жившего в самом начале нашей эры. Эта формула дает определение площади через длины всех сторон треугольника:S = ?*v((a + b + c)*(b + c - a)*(a + c - b)*(a + b - c)).Запись формулы с введением понятия полупериметра упрощается:S = v(p*(p - a)*(p - b)*(p - c)), где p = (a + b + c)/2 - полупериметр.
6
Формула площади треугольника через длину стороны и углы треугольника:S = a^2*sin?*sin?/(2*sin?), где ? и ? – прилежащие углы, а ? – противолежащий угол к стороне a.
7
Для прямоугольного треугольника формула площади упрощается и выглядит следующим образом:S = ?*a*b, т.е. площадь прямоугольного треугольника равна половине произведения длин катетов.
8
Формула площади для равностороннего треугольника:S = (a^2*v3)/4.
9
Формула площади для равнобедренного прямоугольного треугольника:S = ?*(a^2 + b^2), где a и b – катеты треугольника.Кроме того, для любого треугольника справедливо следующее неравенство:S
Видео по теме
Обратите внимание
Треугольники с целочисленными сторонами, площадь которых также равна целому числу, называются треугольниками Герона.
Источники:
- формулы площади треугольника через радиус описанной окружности