Как найти направляющие косинусы вектора

Обозначьте через альфа, бета и гамма углы, образованные вектором а с положительным направлением координатных осей (см. рис.1). Косинусы этих углов называются направляющими косинусами вектора а.

Вам понадобится

• - бумага;
• - ручка.

Инструкция

1. Так как координаты а в декартовой прямоугольной системе координат равны проекциям вектора на координатные оси, тоа1 = |a|cos(альфа), a2 = |a|cos(бета), a3 = |a|cos(гамма). Отсюда: cos (альфа)=a1||a|, cos(бета) =a2||a|, cos(гамма)= a3/|a|. При этом |a|=sqrt(a1^2+ a2^2+ a3^2). Значит cos (альфа)=a1|sqrt(a1^2+ a2^2+ a3^2), cos(бета) =a2|sqrt(a1^2+ a2^2+ a3^2),cos(гамма)= a3/sqrt(a1^2+ a2^2+ a3^2).
2. Следует отметить основное свойство направляющих косинусов. Сумма квадратов направляющих косинусов вектора равна единице.Действительно, cos^2(альфа)+cos^2(бета)+cos^2(гамма)== a1^2|(a1^2+ a2^2+ a3^2)+ a2^2|(a1^2+ a2^2+ a3^2)+ a3^2/(a1^2+ a2^2+ a3^2) = =(a1^2+ a2^2+ a3^2)|(a1^2+ a2^2+ a3^2) = 1.
3. Первый способПример: дано: вектор а={1, 3, 5). Найти его направляющие косинусы.Решение. В соответствии с найденным выпишем: |а|= sqrt(ax^2+ ay^2+ az^2)=sqrt(1+9 +25)=sqrt(35)=5,91. Таким образом, ответ можно записать в следующей форме: {cos(альфа), cos(бета), cos(гамма)}={1/sqrt(35), 3/sqrt (35), 5/(35)}={0,16;0,5;0,84}.
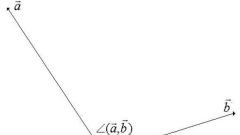
4. Второй способПри нахождении направляющих косинусов вектора а, можно использовать методику определения косинусов углов с помощью скалярного произведения. В данном случае в виду имеются углы между а и направляющими единичными векторами прямоугольных декартовых координат i, j и k. Их координаты {1, 0, 0}, {0, 1, 0}, {0, 0, 1}, соответственно. Следует напомнить, что скалярное произведение векторов определяется так. Если угол между векторами ф, то скалярное произведение двух ветров (по определению) – это число, равное произведению модулей векторов на cosф. (a, b) = |a||b|cos ф. Тогда, если b=i, то (a, i) = |a||i|cos(альфа),или a1 = |a|cos(альфа). Далее все действия выполняются аналогично способу 1, с учетом координат j и k.