Инструкция
1
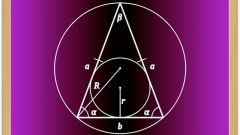
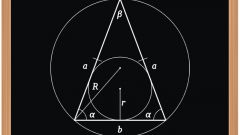
Если из условий задачи кроме длин двух сторон (A и C) в произвольном треугольнике известна и величина угла между ними (β), то примените для нахождения длины третьей стороны (B) теорему косинусов. Сначала возведите длины сторон в квадрат и сложите полученные величины. От этого значения отнимите удвоенное произведение длин этих сторон на косинус известного угла, а из того, что останется, извлеките квадратный корень. В общем виде формулу можно записать так: B=√(A²+C²-2*A*C*cos(β)).
2
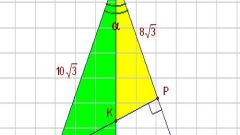
Если дана величина угла (α), лежащего напротив более длинной (A) из двух известных сторон, то начните с вычисления величины угла, противолежащего другой известной стороне (B). Если исходить из теоремы синусов, то его величина должна быть равна arcsin(sin(α)*B/A), а это значит, что величина угла, лежащего напротив неизвестной стороны, будет составлять 180°-α-arcsin(sin(α)*B/A). Следуя для нахождения искомой длины все той же теореме синусов, перемножьте длину наибольшей стороны на синус найденного угла и поделите на синус известного из условий задачи угла: C=A*sin(α-arcsin(sin(α)*B/A))*sin(α).
3
Если дана величина угла (α), прилегающего к стороне неизвестной длины (C), а две другие стороны имеют одинаковые и известные по условию задачи размеры (A), то формула расчета будет значительно проще. Найдите удвоенное произведение известной длины на косинус известного угла: C=2*A*cos(α).
4
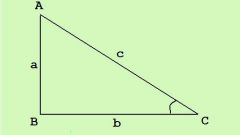
Если рассматривается прямоугольный треугольник и известны длины двух его катетов (А и В), то для нахождения длины гипотенузы (С) воспользуйтесь теоремой Пифагора. Извлеките квадратный корень из суммы возведенных в квадрат длин известных сторон: С=√(А²+В²).
5
Если в расчета длины другого катета исходите из той же теоремы. Извлеките квадратный корень из разности между возведенными в квадраты длинами гипотенузы и известного катета: С=√(C²-В²).