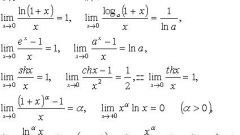Как найти пределы по правилу лопиталя

Краткая историческая справка: маркиз Гийом Франсуа Антуан де Лопиталь обожал математику и был настоящим меценатом для известных ученых. Так Иоганн Бернулли был его постоянным гостем, собеседником и даже сотрудником. Существует предположение, что Бернулли подарил право авторства известного правила Лопиталю в знак благодарности за его услуги. В пользу этой точки зрения говорит тот факт, что доказательство к правилу было официально опубликовано спустя 200 лет еще одним известным математиком Коши.

Вам понадобится

• - ручка;
• - бумага.

Инструкция

1. Правило Лопиталя заключается в следующем: предел отношения функций f(x) и g(x), при х стремящемуся к точке а, равен соответствующему пределу отношения производных этих функций. При этом значение g(a) не равно нулю, как и значение ее производной в этой точке (g’(a)). Кроме того предел g’(a) существует. Аналогичное правило действует и при x, стремящемуся к бесконечности. Таким образом можно записать (см. рис.1):
   
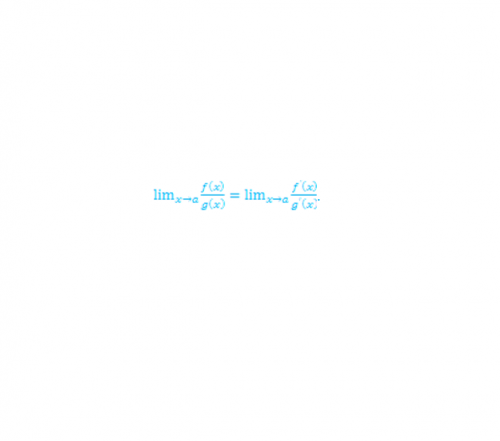
2. Правило Лопиталя позволяет устранять неопределенности типа ноль делить на ноль и бесконечность делить на бесконечность ([0/0], [∞/∞] Если на уровне первых производных вопрос еще не разрешен, следует использовать производные второго и даже большего порядка.
3. Пример 1. Найти предел при х стремящемуся к 0 отношения sin^2(3x)/tg(2x)^2.
   Здесь f(x)=sin^2(3x), g(x)=tg(2x)^2. f’(x)=2•3sin3xcos3x=6sin3xcos3x, g’(x)=4x/cos^2(2x)^2. lim(f’(x)/g’(x))=lim(6sin3x/4x), так как cos(0)=1. (6sin3x)’=18cos3x, (4x)’=4. Итак (см. рис. 2):
   
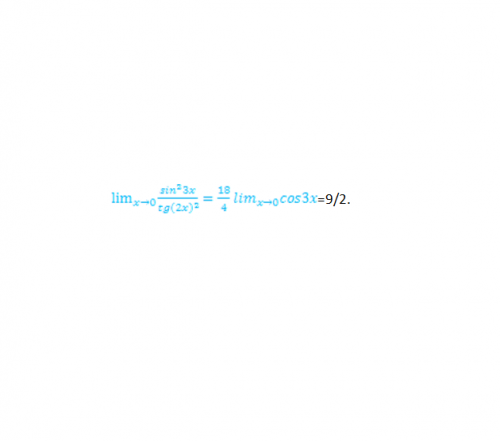
4. Пример 2. Найти предел на бесконечности рациональной дроби (2x^3+3x^2+1)/(x^3+4x^2+5x+7). Ищем отношение первых производных. Это (6x^2+6x)/(3x^2+8x+5). Для вторых производных (12x+6)/(6x+8). Для третьих 12/6=2 (см. рис.3).
   
5. Остальные неопределенности, на первый взгляд, не подлежат раскрытию с помощью правила Лопиталя, т.к. не содержат отношения функций. Однако некоторые предельно простые алгебраические преобразования могут помочь устранить их. Прежде всего можно ноль умножить на бесконечность [0•∞]. Любую функцию q(x) → 0 при х → а можно переписать в виде
   q(x)=1/(1/q(x)) и здесь (1/q(x))→∞.
6. Пример 3.
   Найти предел (см. рис.4)
   В данном случае есть неопределенность ноль умножить на бесконечность. Преобразовав это выражение получите: xlnx=lnx/(1/x), то есть соотношение вида [∞-∞]. Применив правило Лопиталя, получите отношение производных (1/x)/(-1/x2)=-х. Так как х стремится к нулю, , решение предела будет ответ: 0.
   
7. Неопределенность вида [∞-∞], раскрывается, если имеется в виду разность каких-либо дробей. Приведя эту разность к общему знаменателю, получите некоторое отношение функций.
   
   Неопределенности типа 0^∞, 1^∞, ∞^0 возникают при вычислении пределов функций типа p(x)^q(x). В этом случае применяют предварительное дифференцирование. Тогда логарифм искомого предела А примет вид произведения, возможно, что с готовым знаменателем. Если нет, то можно использовать методику примера 3. Главное не забыть записать окончательный ответ в виде е^А (см. рис.5).